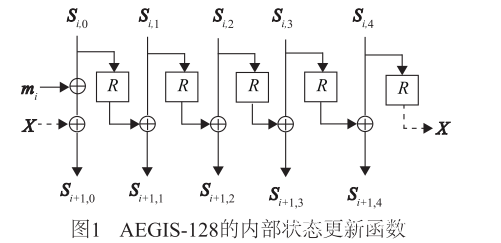
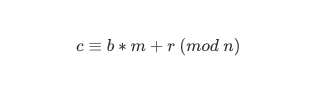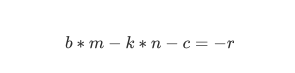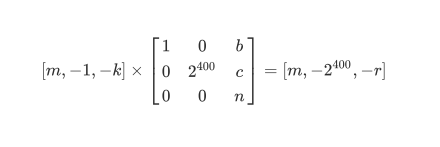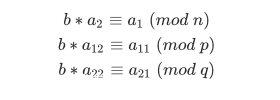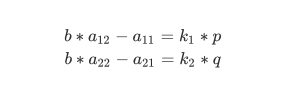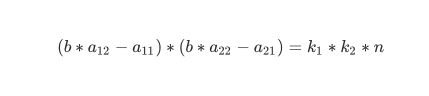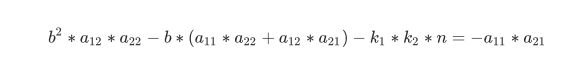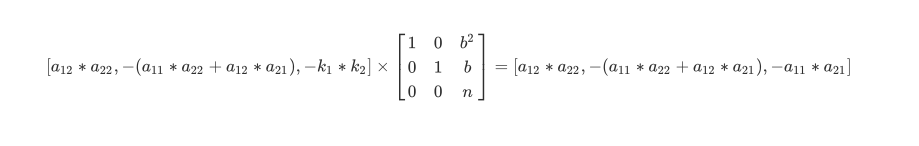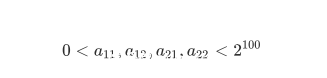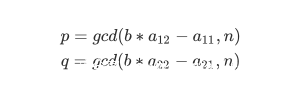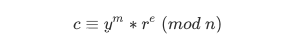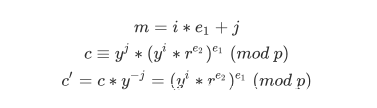垃圾题归档
Table of Contents
Refer:Intnet
2021年中国能源网络安全大赛 #
NumberGame #
e=65537
(p-1)*(q-1)=15743369066365201538689815141217340316571238013087670610561037355773525976258683589473338312326667266426637983360891507450086948913791067841805124377899989037485326133436719169246977060981737084689604571176180431464103979969894191079926052092838806338413905561857239072404009236751128582547515118141940600672935405990869984053032765764114050729270669601890847900632843688927485888918612911073502700067125045327489296133801029104137634700096205588495179191062622618039322093662364377472003903899926787818853067801269953347284657645644433840226628368651915623156258190141632506503179281547840336415021260912890513317032
c=13751833349374257546209411135285092025488474108950873335024549274321086737456294175321120539754112475192176856842163702158437261396059826784892899176923534179915888282864428402789707026830116675021571701648882970445289856088711084812757925707567230381940631064097247655097898810731114605714274641284534967275121251913986394408892187726203752249533094374744765243723455319272657285557501695073422223837888223589541537218910163081228251946239816318853757555291276404517545168694257378212616960758914005374587905274292014917325205163653897110709086078591016724234778570715311198272084303656971117931256882498414761066763
invert(p,q)=63567214271914333094632899333841375147292062018298573854142802911053572390920700513290025348818998146731407276513819782906243535938082361025317768375133584131695102997533625569063205757115454077033715745425720243515047860316309615090852448819151555625882308478246810599114349379924606314715907857949899701531
invert(q,p)=61854206698188431209560015384356189028981002413118973294450748821388080621667741484068895416821294105003859720045449073339567340407545907381482535347338180766054184558875014806879520058753821268699806496142714025634827191809185242495912563928024605815219672974396270176683304596115075405856328836048144151507
给出 $(p-1)(q-1),x=\text{inv}(p,q),y=\text{inv}(q,p),e,c$。
详细推导思路可参考 HITCON 2019 - Lost Modulus Again。
解题脚本:
import gmpy2
from itertools import product
import binascii
from Crypto.Util.number import *
"""
alpha = p' * q' - l
beta = l^2 * [(e * d - 1) / s] + q' * l + p' * l - p' * q' - alpha - l^2
i.e.:
beta = l^2 * {[(e * d - 1) / s] - 1} + l * (q' + p') - alpha - p' * q'
if l,s are correct:
alpha = k * t
beta = k * (p' - l) + t * (q' - l)
i.e:
"""
def alpha_from_pprime_qprime_l(pprime, qprime, l):
return pprime*qprime - l
def beta_from_pprime_qprime_e_d_l_s_alpha(pprime, qprime, e, d, l, s, alpha):
temp1 = e*d - 1
assert temp1 % s == 0
temp2 = ((temp1 // s) - 1) * l * l
temp3 = temp2 + l * (pprime + qprime)
return temp3 - alpha - (pprime*qprime)
def k_t_from_pprime_qprime_l_alpha_beta(pprime, qprime, l, alpha, beta):
a = pprime - l
b = -beta
c = alpha * (qprime - l)
disc = b * b - 4 * a * c
assert gmpy2.is_square(disc)
temp = -b + gmpy2.isqrt(disc)
assert temp % (2*a) == 0
k = temp // (2*a)
assert alpha % k == 0
return k, alpha // k
def brute_k_t_l(pprime, qprime, e, d):
# l, s = 2, 2
ss = [s for s in range(e - 100000, e + 1000000) if s!=0 and (e*d - 1) % s == 0]
for l, s in product(range(1, 5000), ss):
#print(f'l = {l}, s = {s}')
try:
alpha = alpha_from_pprime_qprime_l(pprime, qprime, l)
beta = beta_from_pprime_qprime_e_d_l_s_alpha(pprime, qprime, e, d, l, s, alpha)
k, t = k_t_from_pprime_qprime_l_alpha_beta(pprime, qprime, l, alpha, beta)
return k, t, l
except AssertionError:
continue
if __name__ == "__main__":
e = 65537
fn = 15743369066365201538689815141217340316571238013087670610561037355773525976258683589473338312326667266426637983360891507450086948913791067841805124377899989037485326133436719169246977060981737084689604571176180431464103979969894191079926052092838806338413905561857239072404009236751128582547515118141940600672935405990869984053032765764114050729270669601890847900632843688927485888918612911073502700067125045327489296133801029104137634700096205588495179191062622618039322093662364377472003903899926787818853067801269953347284657645644433840226628368651915623156258190141632506503179281547840336415021260912890513317032
d = gmpy2.invert(e,fn)
pprime = 63567214271914333094632899333841375147292062018298573854142802911053572390920700513290025348818998146731407276513819782906243535938082361025317768375133584131695102997533625569063205757115454077033715745425720243515047860316309615090852448819151555625882308478246810599114349379924606314715907857949899701531
qprime = 61854206698188431209560015384356189028981002413118973294450748821388080621667741484068895416821294105003859720045449073339567340407545907381482535347338180766054184558875014806879520058753821268699806496142714025634827191809185242495912563928024605815219672974396270176683304596115075405856328836048144151507
k, t, l = brute_k_t_l(pprime, qprime, e, d)
lp, lq = qprime + k, pprime + t
assert lp % l == 0, lq % l == 0
p, q = lp // l, lq // l
assert gmpy2.invert(p, q) == pprime, gmpy2.invert(q, p) == qprime
assert gmpy2.is_prime(p), gmpy2.is_prime(q)
N = p*q
c = 13751833349374257546209411135285092025488474108950873335024549274321086737456294175321120539754112475192176856842163702158437261396059826784892899176923534179915888282864428402789707026830116675021571701648882970445289856088711084812757925707567230381940631064097247655097898810731114605714274641284534967275121251913986394408892187726203752249533094374744765243723455319272657285557501695073422223837888223589541537218910163081228251946239816318853757555291276404517545168694257378212616960758914005374587905274292014917325205163653897110709086078591016724234778570715311198272084303656971117931256882498414761066763
flag_decoded = pow(c, d, N)
print(long_to_bytes(flag_decoded))
#b'flag{dP_4nd_dQ_1s_4_exc1tlng_pr0bLEm}'
FillTheBlank #
推公式?
from Crypto.Util.number import *
import gmpy2
import math
a = 16358502146569154805821117102055792126075384391997576813810358118942744612520734385485210209088310766263140599554175000067735671573064419087690267925715334913530155481001158890983091873663077846204509925514040559562873128373049378251801304882824014436351821387973582562165652240535121822439156888350175610414618000437008389187928342072924670546637964062394868004556705496699646429981923137500855492623070913023804420063661041841121617920375160117028363526191248710373415720637387593795136212298387121644166224488964182846517612830649792045421886212347661276446680662471149305906153415890365792363053111611744767732723
b = "**********"
d = 1004034638166310792730607806775703553124564601554345421260673
flag="flag{*************}".encode("utf-8")
m = bytes_to_long(flag)
z = "**********"
rb = gmpy2.invert(b, p) #p应为a
rd = gmpy2.invert(d, p) #p应为a
x = rb*rd
c = (m + z * rb * d % a)%a
assert(x==6315659043002030386732628047413448608037014021450055783529151485037069834363316696715574624507364755209361330204858147422873261866250183596759294051863367248800298182067900158706847792801508096127972864438349393635089442050383307416911012903769591812354414290225858817653700560363386018244490076357373032578412217266586094695255045411910123500620718125148007865650934761243821251725823364164494857358344030633984045814182753879152597382860304163779884435644346012876829684180445183686922253767338719485395107909704323571278192414797079570675523716981179479127876875936828316228191746093521584500893126198631718691478)
assert(c == 13596888613593355909989922489890598098147006404940300566769884949973269155719149670825677093684865700611084990815597885910353735947129944271345041538903031681298587672182524580124290627382140539264797169742520543929318842181890234622629255911624719400312152476306595541663238469772749767491911131691767357337344670678126067823905376191196367985379783363614691429132347967869598160549130755596368301366502209859435570988428790501722994265227987470237460083210385323943246674820772425514186206511159274330451656105100385024137631498256411854720506611702496670593426888793357086314109878603547497784715623917384308274129)
assert(log(d)/log(2)<=200)
assert(log(z)/log(2)<=1024)
推导:
由 $rb \equiv b^{-1} \pmod a$ 和 $rd \equiv d^{-1} \pmod a$ ,有 $rb \cdot b \cdot rd \cdot d = x \cdot b \cdot d \equiv 1 \pmod a$。
故求出 $b \equiv (x \cdot d)^{-1} \pmod a$,$rb \equiv b^{-1} \pmod a$。
又 $c = (m+z \cdot rb \cdot d) \bmod a$,构造格 $L=\begin{bmatrix} 1 & rb \cdot d \ 0 & a \end{bmatrix}$,利用LLL算法求解:
a = 16358502146569154805821117102055792126075384391997576813810358118942744612520734385485210209088310766263140599554175000067735671573064419087690267925715334913530155481001158890983091873663077846204509925514040559562873128373049378251801304882824014436351821387973582562165652240535121822439156888350175610414618000437008389187928342072924670546637964062394868004556705496699646429981923137500855492623070913023804420063661041841121617920375160117028363526191248710373415720637387593795136212298387121644166224488964182846517612830649792045421886212347661276446680662471149305906153415890365792363053111611744767732723
d = 1004034638166310792730607806775703553124564601554345421260673
x = 6315659043002030386732628047413448608037014021450055783529151485037069834363316696715574624507364755209361330204858147422873261866250183596759294051863367248800298182067900158706847792801508096127972864438349393635089442050383307416911012903769591812354414290225858817653700560363386018244490076357373032578412217266586094695255045411910123500620718125148007865650934761243821251725823364164494857358344030633984045814182753879152597382860304163779884435644346012876829684180445183686922253767338719485395107909704323571278192414797079570675523716981179479127876875936828316228191746093521584500893126198631718691478
c = 13596888613593355909989922489890598098147006404940300566769884949973269155719149670825677093684865700611084990815597885910353735947129944271345041538903031681298587672182524580124290627382140539264797169742520543929318842181890234622629255911624719400312152476306595541663238469772749767491911131691767357337344670678126067823905376191196367985379783363614691429132347967869598160549130755596368301366502209859435570988428790501722994265227987470237460083210385323943246674820772425514186206511159274330451656105100385024137631498256411854720506611702496670593426888793357086314109878603547497784715623917384308274129
import gmpy2
b = gmpy2.invert(x*d,a)
rb = gmpy2.invert(b,a)
rd = gmpy2.invert(d,a)
h = rb*d%a
p = a
v1 = vector(ZZ, [1, h])
v2 = vector(ZZ, [0, p])
m = matrix([v1,v2]);
f, g = m.LLL()[0]
f, g = -f, -g
#print(f, g)
a = f*c % p % g
m = a * inverse_mod(f, g) % g
print(bytes.fromhex(hex(m)[2:]))
#b'flag{we1c0mE_t0_cr4aK_mE!}'
GKCTFxDASCTF应急挑战杯 #
Random #
import random
from hashlib import md5
def get_mask():
file = open("random.txt","w")
for i in range(104):
file.write(str(random.getrandbits(32))+"\n")
file.write(str(random.getrandbits(64))+"\n")
file.write(str(random.getrandbits(96))+"\n")
file.close()
get_mask()
flag = md5(str(random.getrandbits(32)).encode()).hexdigest()
print(flag)
根据 random.txt 中104组 random.getrandbits() 函数输出值,利用预测工具
Mersenne Twister Predictor 来求出下一个随机数:
import random
from mt19937predictor import MT19937Predictor
from hashlib import md5
predictor = MT19937Predictor()
file = open("random.txt","r").readlines()
c1 = []
c2 = []
c3 = []
for k in range(0,len(file),3):
c1 += [int(file[k].strip())]
c2 += [int(file[k+1].strip())]
c3 += [int(file[k+2].strip())]
for k in range(104):
predictor.setrandbits(c1[k], 32)
predictor.setrandbits(c2[k], 64)
predictor.setrandbits(c3[k], 96)
print(md5(str(predictor.getrandbits(32)).encode()).hexdigest())
#14c71fec812b754b2061a35a4f6d8421
RSA #
Just RSA!
from Crypto.Util.number import *
from sympy import nextprime
import gmpy2
import random
def encode (p1,p2,e):
not_hint = (p1 + 1) * (p2 + 1)
S = gmpy2.invert(e, not_hint)
not_p = S%(p1+1)
return not_p
flag = b'Neepu{********************}'
flag = bytes_to_long(flag)
p = getPrime(512)
q = getPrime(512)
n = p*q
e = nextprime(random.randint(1,1000))
d = gmpy2.invert(e, (p-1)*(q-1))
c = pow(flag, e, n)
print(c)
print(n)
m = encode(p, q, e)
c1 = pow(m, 7, n)
c2 = pow(m+e, 7, n)
print(c1)
print(c2)
'78543767285872349029076059073458316000847341792088805258173041942425687239313215276670106926320359777962661495032475004417723103701253550583245518206305422982968675291500865382213182669036827898932991063338163290845510339896689210314509493839746410486257998875782496654704288722251878269643040214139429715671'
'91995272927105081122659192011056020468305570748555849650309966887236871318156855318666540461669669247866754568189179687694315627673545298267458869140096224628114424176937828378360997230874932015701507629238213240839370628366083111028544554453150572165461450371411341485911677167168492357154684642531577228543'
'10186066785511829759164194803209819172224966119227668638413350199662683285189286077736537161204019147791799351066849945954518642600518196927152098131117402608793752080104402893792812059620726950782670809837962606250674588612783027976958719051829085903720655233948024280118985875980227528403883475592567727892'
'46182103994299145562022812023438495797686077104477472631494150222038404419414100727667171290098624214113241032861128455086601197239761085752413519627251290509474327611253599768650908336142621210005389246714504358370629231557080301516460985022782887233790302054696967900384601182742759555421864610431428746119'
两部分:
第一部分 $n=pq,c=\text{flag}^e \bmod n$,
第二部分 $m=\text{enc}(p,q,e),c_1=m^7 \bmod n,c_2=(m+e)^7 \bmod n$。
先解第二部分,利用Related Message Attack求解 $m$,由于 $e$ 未知且 $e<1010$,爆破 $e$ 求出 $m$:
import binascii
def attack(c1, c2, n, e):
PR.<x> = PolynomialRing(Zmod(n))
g1 = (x)^7 - c1
g2 = (x+e)^7 - c2
def gcd(g1, g2):
while g2:
g1, g2 = g2, g1 % g2
return g1.monic()
return -gcd(g1, g2)[0]
c1 = 10186066785511829759164194803209819172224966119227668638413350199662683285189286077736537161204019147791799351066849945954518642600518196927152098131117402608793752080104402893792812059620726950782670809837962606250674588612783027976958719051829085903720655233948024280118985875980227528403883475592567727892
c2 = 46182103994299145562022812023438495797686077104477472631494150222038404419414100727667171290098624214113241032861128455086601197239761085752413519627251290509474327611253599768650908336142621210005389246714504358370629231557080301516460985022782887233790302054696967900384601182742759555421864610431428746119
n = 91995272927105081122659192011056020468305570748555849650309966887236871318156855318666540461669669247866754568189179687694315627673545298267458869140096224628114424176937828378360997230874932015701507629238213240839370628366083111028544554453150572165461450371411341485911677167168492357154684642531577228543
for e in range(1,1000):
m = attack(c1, c2, n, e)
try:
if pow(m,7,n) == c1:
print((e,m))
except:
pass
#结果:(71, 129256555243625096140386916253259867206651269142565502540823654159666398099455456877012993395632742360829588042575108302297567291349420390228163587340859)
#e = 71
#m = 129256555243625096140386916253259867206651269142565502540823654159666398099455456877012993395632742360829588042575108302297567291349420390228163587340859
又 $m=\text{enc}(p,q,e)$,即 $eS=ed \equiv 1 \pmod {(p+1)(q+1)},dp=S \bmod (p+1)=d \bmod (p+1)$,
由于 $e \cdot dp \equiv e \cdot d \equiv 1 \pmod {(p+1)}$,有 $e \cdot dp-1=k \cdot (p+1)$,
比较 $e \cdot dp$ 与 $p$ 比特位数相近,故 $k$ 值不大,
爆破 $k$,当同时满足 $(e \cdot dp-1) \bmod k =0$ 和 $n \bmod \Big(\cfrac{e \cdot dp-1}{k}-1\Big)$ 时,$n$ 成功分解。
n = 91995272927105081122659192011056020468305570748555849650309966887236871318156855318666540461669669247866754568189179687694315627673545298267458869140096224628114424176937828378360997230874932015701507629238213240839370628366083111028544554453150572165461450371411341485911677167168492357154684642531577228543
dp = 129256555243625096140386916253259867206651269142565502540823654159666398099455456877012993395632742360829588042575108302297567291349420390228163587340859
e = 71
c = 78543767285872349029076059073458316000847341792088805258173041942425687239313215276670106926320359777962661495032475004417723103701253550583245518206305422982968675291500865382213182669036827898932991063338163290845510339896689210314509493839746410486257998875782496654704288722251878269643040214139429715671
for k in range(1,10000):
if (e*dp-1)%k == 0:
p = (e*dp-1)//k-1
if n%p == 0:
q = n//p
print((k,p,q))
最后常规RSA求得flag。
红明谷杯数据安全大赛技能场景赛 #
ezCRT #
Chinese Remainder Theorem is fantastic
from Crypto.Util.number import * import gmpy2 from random import shuffle flag = b"flag is here" def shuffle_flag(s): str_list = list(s) shuffle(str_list) return ''.join(str_list) nl = [] el = [] count = 0 while count != 5: p = getPrime(512) q = getPrime(512) n = p * q phi = (p - 1) * (q - 1) d = gmpy2.next_prime(bytes_to_long(flag)) e = gmpy2.invert(d, phi) nl.append(n) el.append(int(e)) count += 1 print(nl) print(el) cl = [] flag = shuffle_flag(flag.decode()).encode() for i in range(len(nl)): cl.append(pow(bytes_to_long(flag), el[i], nl[i])) print(cl)
五组 $n,e$,共私钥 $d$,用LLL算法打。发现 $n$ 都已帮从小到大排好序,一步到位。
由于 d = gmpy2.next_prime(bytes_to_long(flag)),求出 $d$ 后往回遍历拿到flag。
#Sage
from gmpy2 import *
n =
e =
c =
M=iroot(int(n[4]),int(2))[0]
a = [0]*6
a[0] = [M,e[0],e[1],e[2],e[3],e[4]]
a[1] = [0,-n[0],0,0,0,0]
a[2] = [0,0,-n[1],0,0,0]
a[3] = [0,0,0,-n[2],0,0]
a[4] = [0,0,0,0,-n[3],0]
a[5] = [0,0,0,0,0,-n[4]]
Mat = matrix(ZZ,a)
Mat_LLL = Mat.LLL()
d = abs(Mat_LLL[0][0]) // M
for k in range(1500):
print(bytes.fromhex(hex(d-k)[2:]))
Crypto_System #
从[CyBRICS 2020 - Too Secure]( http://ctfteam.com/writeup/8/Too Secure)魔改的Pedersen加密,算法描述:

已知信息 $m_1,m_2$和 $m_1$ 的 $r_1$,$m_1$ 通过因子 $r_1$ 加密得到 $c_1$,需要求出因子 $r_2$,使得 $m_2$ 通过 $r_2$ 加密得到的 $c_2$ 与 $c_1$ 相同,即产生碰撞。
对于待加密信息 $m_1$,$c_1=g^{m_1}h_1^{r_1}$,注意到 $h_1=g^{a_1}$,故 $c_1=g^{m_1+a_1r_1}$;
要碰撞信息 $m_2$ 的因子 $r_2$ 应满足 $c_2=c_1$,即 $m_1+a_1r_1 \equiv m_2+a_2r_2 \pmod {\varphi(p)}$,
又 $q$ 为 $g$ 的阶,所以有 $m_1+a_1r_1 \equiv m_2+a_2r_2 \pmod q$,
故 $r_2 \equiv (m_1+a_1r_1-m_2) \pmod q$,即可求出 $r_2$。
Exp:
#python2
from pwn import *
from parse import *
from pwnlib.util.iters import bruteforce
import string
from hashlib import sha256
from Crypto.Util.number import *
import hashlib
from gmpy2 import gcd,invert
def brute_force(prefix,s):
return bruteforce(lambda x:sha256(x+prefix).hexdigest()==s,string.ascii_letters+string.digits,length=4,method='fixed')
p = 12039102490128509125925019010000012423515617235219127649182470182570195018265927223
g = 10729072579307052184848302322451332192456229619044181105063011741516558110216720725
def int2str(data, mode="big"):
if mode == "little":
return sum([ord(data[_]) * 2 ** (8 * _) for _ in range(len(data))])
elif mode == "big":
return sum([ord(data[::-1][_]) * 2 ** (8 * _) for _ in range(len(data))])
def get_parameter(m):
x = int2str(m, 'little')
y = pow(g, x, p)
a = bytes_to_long(hashlib.sha256(long_to_bytes(y).rjust(128, "\0")).digest())
b = pow(a, a, p - 1)
h = pow(g, b, p)
return x, y, h, b
def sign(m, r):
x, y, h, b = get_parameter(m)
s = (y * pow(h, r, p)) % p
return s
def verify(m, r, s):
x, y, h, b = get_parameter(m)
if s == ((y * pow(h, r, p)) % p):
return True
else:
return False
r=remote('139.129.98.9',30001)
data = r.recvline()
prefix, s = parse("sha256(XXXX+{}) == {}",data)
r.recvuntil('Give me XXXX:')
r.sendline(brute_force(prefix,s))
r.recvline()
r.recvline()
m1 = long_to_bytes(int(parse("Here is the frist message(64 bytes):{}",r.recvline())[0],16))
m2 = long_to_bytes(int(parse("Here is the second message(64 bytes):{}",r.recvline())[0],16))
r1 = int(parse("The frist message's 'r':{}",r.recvline())[0])
print(m1)
print(m2)
#sage solve order q: g^q=1(mod p)
q = 1039300813886545966418005631983853921163721828798787466771912919828750891
assert(pow(g, q, p) == 1)
assert(gcd(q, p-1) == q)
M1,y1,h1,b1 = get_parameter(m1)
M2,y2,h2,b2 = get_parameter(m2)
s1 = sign(m1, r1)
p1 = b1*r1
p2 = M2-M1
p3 = p1-p2
p4 = invert(b2,q)
r2 = (p3*p4)%q
s2 = sign(m2,r2)
if s1==s2:
print('r1 = '+str(r1))
print('r2 = '+str(r2))
print('s1 = '+str(s1))
print('s2 = '+str(s2))
print('verify(m2,r2,s2) = '+str(verify(m2,r2,s2)))
r.recvuntil('Please choice your options:')
r.sendline('3')
r.sendlineafter('Please give me the (r,s) of the second message:','('+str(r2)+','+str(s2)+')')
print(r.recvall())
ROARCTF2020 #
Reverse #
参考 https://kt.gy/blog/2015/10/asis-2015-finals-rsasr/ 因为p和q是二进制顺序相反的素数,所以p的每一位都和q有关系。所以我们可以尝试遍历p的二进制,通过判断生成的p与q再进行迭代。具体代码如下:
n = 158985980192501034004997692253209315116841431063210516613522548452327355222295231366801286879768949611058043390843949610463241574886852164907094966008463721486557469253652940169060186477803255769516068561042756903927308078335838348784208212701919950712557406983012026654876481867000537670622886437968839524889
def Brute_force(a,b,k):
if k == 256:
if a*b==n:
print (a,b)
return 0
for i in range(2):
for j in range(2):
a1=a+i*(2**(511-k))+j*(2**k)
b1=b+j*(2**(511-k))+i*(2**k)
if a1*b1>n:
continue
if (a1+2**(511-k))*((b1+2**(511-k)))< n:
continue
if (a1*b1)%(2**(k+1)) != n%(2**(k+1)):
continue
Brute_force(a1,b1,k+1)
return 0
Brute_force(0,0,0)
ECDSA #
这道题贼狠,源码都不给,来看一看MENU叭
[DEBUG] Received 0xd bytes:
b'Give me XXXX:'
[DEBUG] Sent 0x5 bytes:
b'bwUI\n'
[DEBUG] Received 0x4f bytes:
b'Hello,guys!Welcome to my ECC Signature System!I promise no one can exploit it!\n'
[DEBUG] Received 0x269 bytes:
b'Howevers if you can exploit it in 10 times,I will give what you want!\n'
b'Here is the frist message(64 bytes):fipoN9jy/*@~J:] PcZY8{&X!7v+\\duTln_#k(WK^Q2L)<SbM$-V=Ex3Uw|h,%}F\n'
b'Here is the second message(64 bytes):%wh-(xJ4kR+7<^Zv9,Ol\\Kp/&"FHbc_ D@Y*mSos}V?.#L{!3B8QiP=nqCI[y:X2\n'
b'Try to calculate the same signature for this two messages~\n'
b'(((Notice: curve = SECP256k1, hashfunc = sha1)))\n'
b'\n'
b'ECC Signature System:\n'
b' 1. Show your pubkey\n'
b' 2. Generate new prikey\n'
b' 3. Update your pubkey\n'
b' 4. Sign a message\n'
b' 5. Verify a message\n'
b' 6. Exploit\n'
b' 7. Exit\n'
b'\n'
b'You have only 10 times to operate!\n'
b'Please choice your options:'
根据题目名这是一个ECDSA的签名系统,完了呢要求是给这他提供的两个msg签名,不仅验证要通过,而且签名还得一样。
先来看看这几个功能,
功能1是显示公钥,(可能要利用)
功能2是重新生成一个私钥,(应该是没用的,没啥意义,生成后就是告诉你更新后的公钥)
功能3是更新你的公钥,你来输入(这个肯定有点用)
功能4是帮你签个名 (也许用得上)
功能5是验证签名 (可以,但没必要)
功能6就是整完了用来获取flag的了。
六个功能一眼看来也就这个功能3可以用了。这里需要一点前置知识(现查就可以了,一样的),就是ECDSA签名的验证规则
这种 资料CSDN一抓一大把。

image-20201207214850259
最后是判断 v = r,即 X.x = dG.x ,我们可以把验证公式提取出来,也即 $es^{-1}G + rs^{-1}Q = dG$
注意到由于验证用的是公钥Q,然后题目是提供篡改公钥这个功能的,我们知道ECDSA中$Q = kG$, 其中k是私钥,那么其实等价于我们是可以篡改私钥的,即我们用自己的私钥去给一个信息签名,完了后把用于验证的公钥给改成我们自己的公钥,验证同样也是可以通过的。那么整个过程系统的私钥都不参与了。
解决了签名验证的问题,剩下来就是解决如何让他们的签名保持一致了。
回到验证公式 $es^{-1}G + rs^{-1}Q = dG$
其中e是我们的消息,可以看作已知常数,r和s是我们能控制的,G是固定的,Q是公钥,也是我们自己决定,d是签名时用的随机数,整个签名的过程我们都能掌握,自然d也有我们决定,然后d会决定r,因为r = dG.x, 那么r也就固定下来了,只剩Q和s了。
我们把公式约一约,去掉G后就是 $es^{-1} + rs^{-1}k = d => e + rk = ds => s = (e + rk)*d^{-1}$
由于两个msg的s要保持一直,那么我们构造的等式就是$ (e_1 + rk) * d^{-1} = (e_2 + rk) * d^{-1}$
很显然啊,因为d不能等于0,这等式不可能成立啊,于是陷入僵局。
但这里我们忘了一个很重要的性质,就是,我们最后验证的是v = r,而r是什么,r = dG.x,我们要知道的是,椭圆曲线是一个关于x轴对称的图形,所以其实 r = -dG.x。华点都发现了,这题就解决了,
等式变为$ (e_1 + rk) * d^{-1} = (e_2 + rk) * (-d)^{-1}$
化成同余式就是$ (e_1 + rk) * d^{-1} \equiv (e_2 + rk) * (-d)^{-1} \pmod{n}$
有 $e_1 + rk \equiv -e_2 -rk\pmod{n}$
有 $k \equiv \frac{-e1-e2}{2r}\pmod{n}$
然后怕【我们去查一下这条曲线的 参数即可
参考脚本
from pwn import *
from Crypto.Util.number import *
sh=remote("139.129.98.9","30002")
from pwnlib.util.iters import mbruteforce
from hashlib import sha256
import hashlib
from math import gcd
context.log_level = 'debug'
a=0
b=7
q=0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
gx=0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
gy=0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
order=0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
ecc = EllipticCurve(GF(q), [a,b])
G = ecc(gx,gy)
import hashlib
def sha1(content):
return hashlib.sha1(content).digest()
def proof_of_work(sh):
sh.recvuntil("XXXX+")
suffix = sh.recvuntil(')').decode("utf8")[:-1]
log.success(suffix)
sh.recvuntil("== ")
cipher = sh.recvline().strip().decode("utf8")
proof = mbruteforce(lambda x: sha256((x + suffix).encode()).hexdigest() == cipher, string.ascii_letters + string.digits, length=4, method='fixed')
sh.sendlineafter("Give me XXXX:", proof)
proof_of_work(sh)
sh.recvuntil("Here is the frist message(64 bytes):")
msg1 = sh.recvuntil("\n")[:-1]
sh.recvuntil("Here is the second message(64 bytes):")
msg2 = sh.recvuntil("\n")[:-1]
message = hex(bytes_to_long(msg1))[2:]
e1=bytes_to_long(sha1(msg1))
e2=bytes_to_long(sha1(msg2))
######################################################
#解题核心
#pubkey = sh.recvuntil("\n")[:-2].decode()
#r=[d * G].x
d=12321
r=int((d*G)[0])
new_k = ((-e1-e2)*inverse(2*r,order))%order
new_Q = new_k * G
new_S = ((e1 + new_k*r)*inverse(d,order))%order
newpubkey = hex(new_Q[0]).replace("0x","").rjust(64,"0")+hex(new_Q[1]).replace("0x","").rjust(64,"0")
newsignature = hex(r).replace("0x","").rjust(64,"0")+hex(new_S).replace("0x","").rjust(64,"0")
######################################################
sh.recvuntil("Please choice your options:")
sh.sendline("3")
sh.recvuntil("Please give me your public_key(hex):")
sh.sendline(newpubkey)
sh.recvuntil("Please choice your options:")
sh.sendline("6")
sh.recvuntil("Please give me the signature(hex) of the frist message:\n")
sh.sendline(newsignature)
sh.recvuntil("Please give me the signature(hex) of the second message:\n")
sh.sendline(newsignature)
sh.interactive()
<
>
ByteCTF #
noise #
需要前置知识或了解:中国剩余定理
task.py
#!/usr/bin/env python3
from os import urandom
from random import choices
from hashlib import sha256
import signal
import string
import sys
def getrandbits(bit):
return int.from_bytes(urandom(bit >> 3), "big")
def proof_of_work() -> bool:
alphabet = string.ascii_letters + string.digits
nonce = "".join(choices(alphabet, k=8))
print(f'SHA256("{nonce}" + ?) starts with "00000"')
suffix = input().strip()
message = (nonce + suffix).encode("Latin-1")
return sha256(message).digest().hex().startswith("00000")
def main():
signal.alarm(60)
if not proof_of_work():
return
secret = getrandbits(1024)
print("Listen...The secret iz...M2@9c0f*#aF()I!($Ud3;J..."
"Hello?...really noisy here again...God bless you get it...")
for i in range(64):
try:
op = input().strip()
num = input().strip()
except EOFError:
return
if not str.isnumeric(num):
print("INVALID NUMBER")
continue
num = int(num)
if op == 'god':
print(num * getrandbits(992) % secret)
elif op == 'bless':
if num == secret:
try:
from datetime import datetime
from flag import FLAG
except Exception as e:
FLAG = "but something is error. Please contact the admin."
print("CONGRATULATIONS %s"%FLAG)
return
print("WRONG SECRET")
main()
还好,第一题代码量不大,不错不错。看一看,这一题功能很简单,你输入一个数字,他返回给你一个,你的数字 乘上一个992bit的 随机数字 模上一个1024bit的secret 的结果。当然,每次连接上后生成的secret是随机的,但是连上一次,可以交互64次,此时secret是保持不变的。算上你需要一次交互来获取flag,那么就是需要在63次之内“猜”到这个随机生成的secret。
好的,上式子,我们知道中国剩余定理是这样子的
$m \equiv c_1 \pmod {n_1}$ $m = c_1+k_1n_1$
$m \equiv c_2 \pmod {n_2}$ 等价于 $m = c_2+k_2n_2$
$m \equiv c_3 \pmod {n_3}$ $m = c_3+k_3n_3$
注意这里的模是n,他们彼此互素,然后利用中国剩余定理就可以恢复m(如果m的bit位数小于所有n的bit位数之和的话)
此时,如果k都等于1,那么,
$m = c_1+n_1$ $m = n_1+c_1$
$m = c_2+n_2$ 等价于 $m = n_2+c_2$
$m = c_3+n_3$ $m = n_3+c_3$
此时n和c就好像等价了,并不能知道模数到底是哪个,换一个说法就是,n和c都可以看作是模数
我们再回到这道题本身,设我们发送的值是$n_1,n_2,n_3$,secret为s,返回的值是$c_1,c_2,c_3$,
那么就会有这么些式子
$n_1 * randnum1 \equiv c_1 \pmod s = c_1+k_1s$
$n_2 * randnum2 \equiv c_2 \pmod s= c_2+k_2s$
$n_3 * randnum3 \equiv c_3 \pmod s= c_3+k_3s$
此时如果k值都为1,再挪个位置,那么就有
$s = n_1 * randnum1- c_1$
$s = n_2* randnum2 - c_2$
$s = n_3 * randnum3- c_3$
此时如果我们式子两边去一个模$n_1,n_2,n_3$
$s \equiv- c_1 \pmod{n_1}$
$s \equiv- c_2 \pmod{n_2}$
$s \equiv- c_3 \pmod{n_3}$
这不就是中国剩余定理形式么?所以当等于1,我们就可以利用中国剩余定理来恢复这个secret
需要满足的条件就是,$n*randnum = c+s$,还有就是n的bit位数之和要大于s的bit位数即1024
当然,这就需要运气了,因为他远程生成的乘数是随机的992bit数字(当然是有可能会小于992bit的),而s是1024bit的数字,所以我们要发送的n大概就是32bit的素数,32*32=1024,所以在63次交互内我们需要服务器生成32个随机数是“好”的,所谓”好””就是要让这个k正好等于1。
我们也可以先本地简单的测一测,可以选择比较小的数给他乘,这样子的k大概率会是0或者1,而0比较好判断,直接判断返回的值是否被我们发送过去的数整除就可以了。而是否正好等于1我们是无法判断的,但凡一组数据插入了一个让k不等于1或者0的数,那么整组数据就作废了。所以我们发送尽量小的数n,让k值大概率只落在0或者1上。
测试代码:
from random import *
primes = [4294966427, 4294966441, 4294966447, 4294966477, 4294966553, 4294966583, 4294966591, 4294966619, 4294966639, 4294966651, 4294966657, 4294966661, 4294966667, 4294966769, 4294966813, 4294966829, 4294966877, 4294966909, 4294966927, 4294966943, 4294966981, 4294966997, 4294967029, 4294967087, 4294967111, 4294967143, 4294967161, 4294967189, 4294967197, 4294967231, 4294967279, 4294967291]
for _ in range(20):
secret = getrandbits(1024)
for num in primes:
print(num * getrandbits(992) // secret),
print
这里我们选择固定了随机数,然后经过20次的测试,下面是测试结果

image-20201102145925061
可以发现,生成的随机数似乎也具有一定程度的局部性,当k出现7,8这样比较大的数的时候,几乎整组的k都比较大,但大部分情况下,由于我们输入的素数比较小,还是只有0和1的情况偏多,但一般也是0偏多,所以,,看脸了,只要有一半以上的1,我们就成功了。
解题流程: #
- 确定63个比较小的素数
- 把这些值发送过去
- 收到的值进行一个判断,是否被自己发过去的数整除,是就扔掉,否则就存起来
- 存起来的数超过32个就可以进行CRT尝试恢复secret
- 发送secret过去验证,要是没拿到flag就回到第2步,如此循环往复,加油吧,看你的脸了!
exp:
from pwn import *
from hashlib import sha256
from tqdm import tqdm
from Crypto.Util.number import *
def GCRT(mi, ai):
assert (isinstance(mi, list) and isinstance(ai, list))
curm, cura = mi[0], ai[0]
for (m, a) in zip(mi[1:], ai[1:]):
d = int(GCD(curm, m))
c = a - cura
assert (c % d == 0)
K = c // d * inverse(curm // d, m // d)
cura += curm * K
curm = curm * m // d
cura %= curm
return cura % curm, curm
def proof_of_work(sh):
sh.recvuntil("SHA256(\"")
nonce = sh.recv(8)
sh.recvuntil('with \"00000\"')
for a in tqdm(range(0x30, 0x7f)):
for b in range(0x30, 0x7f):
for c in range(0x30, 0x7f):
for d in range(0x30, 0x7f):
rest = chr(a) + chr(b) + chr(c) + chr(d)
m = (nonce.decode('latin1') + rest).encode("Latin-1")
if sha256(m).digest().hex().startswith("00000"):
sh.sendline(rest)
sh.recvuntil('again...God bless you get it...')
return
def io(sh, num):
sh.sendline('god')
sh.sendline(str(num))
tmp = sh.recvuntil('\n')
if len(tmp) > 100:
return int(tmp)
else:
return int(sh.recvuntil('\n'))
primes = [4294966427, 4294966441, 4294966447, 4294966477, 4294966553, 4294966583, 4294966591, 4294966619, 4294966639, 4294966651, 4294966657, 4294966661, 4294966667, 4294966769, 4294966813, 4294966829, 4294966877, 4294966909, 4294966927, 4294966943, 4294966981, 4294966997, 4294967029, 4294967087, 4294967111, 4294967143, 4294967161, 4294967189, 4294967197, 4294967231, 4294967279, 4294967291]
for i in range(2**10):
sh = remote("182.92.153.117", 30101)
proof_of_work(sh)
length = 32
c = []
index = 0
for i in range(63):
tmp = io(sh, primes[index])
if tmp%primes[index] !=0: //这个判断是剔除k等于0的情况
c.append(-1 * tmp)
index += 1
if index >= 32: //如果超过32个数的k不等于0,我们就可以拿来用了,但也不确定是否这32个数都为1
break
if index < 32:
continue
secret = GCRT(primes, c)[0]
sh.sendline('bless')
sh.sendline(str(secret))
tmp = sh.recvuntil('\n')
if len(tmp) < 5:
tmp = sh.recvuntil('\n')
if b'WRONG' in tmp:
sh.close()
continue
print(tmp)
sh.interactive()
threshold #
需要前置知识或了解:椭圆曲线相关性质
from gmssl import func, sm2
#from flag import FLAG
flag="Congratulations!"
sm2p256v1_ecc_table = {
'n': 'FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123',
'p': 'FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF',
'g': '32c4ae2c1f1981195f9904466a39c9948fe30bbff2660be1715a4589334c74c7' +
'bc3736a2f4f6779c59bdcee36b692153d0a9877cc62a474002df32e52139f0a0',
'a': 'FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC',
'b': '28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93',
}
n = 'FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123'
G = '32c4ae2c1f1981195f9904466a39c9948fe30bbff2660be1715a4589334c74c7' \
'bc3736a2f4f6779c59bdcee36b692153d0a9877cc62a474002df32e52139f0a0'
def sign(tsm2):
data = func.random_hex(len(n))
k1_str = func.random_hex(len(n))
print(tsm2.send_p1(data, k1_str))
backdoor = input('backdoor:').strip()
result = tsm2.output_p1(k1_str, backdoor)
print(result)
def verify(tsm2):
message = input('msg:').strip().encode().strip(b'\x00')
sign = input('sign:').strip().encode().strip(b'\x00')
check = tsm2.verify(sign, message)
if check is True and message == b'Hello, Welcome to ByteCTF2020!':
print(FLAG)
else:
print(check)
class TSM2(object):
def __init__(self, sk):
ecc_table = sm2p256v1_ecc_table
self.ecc_table = ecc_table
self.n = int(ecc_table['n'], 16)
self.para_len = len(ecc_table['n'])
self.ecc_a3 = (int(ecc_table['a'], base=16) + 3) % int(ecc_table['p'], base=16)
self.sk = int(sk, 16)
self.pk = self._kg(self.sk, ecc_table['g'])
self.sks = int(func.random_hex(self.para_len), 16)
self.pks = pow((self.sk + 1) * self.sks, self.n - 2, self.n) % self.n
def send_p1(self, data, k1_str):
e = int(data, 16)
k1 = int(k1_str, 16)
k1 = k1 % self.n
R1 = self._kg(k1, self.ecc_table['g'])
return '%064x%0128s' % (e, R1)
def output_p1(self, k1_str, r_s2_s3):
r = int(r_s2_s3[0:self.para_len], 16)
s2 = int(r_s2_s3[self.para_len:2 * self.para_len], 16)
s3 = int(r_s2_s3[2 * self.para_len:], 16)
k1 = int(k1_str, 16)
d1 = self.sks、
s = (d1 * k1 * s2 + d1 * s3 - r) % self.n
if s == 0 or s == (self.n - r):
return None
return '%064x%064x' % (r, s)
def verify(self, Sign, data):
r = int(Sign[0:self.para_len], 16)
s = int(Sign[self.para_len:2 * self.para_len], 16)
e = int(data.hex(), 16)
t = (r + s) % self.n
if t == 0:
return 0
P1 = self._kg(s, self.ecc_table['g'])
P2 = self._kg(t, self.pk)、
if P1 == P2:
P1 = '%s%s' % (P1, 1)
P1 = self._double_point(P1)
else:
P1 = '%s%s' % (P1, 1)
P1 = self._add_point(P1, P2)
P1 = self._convert_jacb_to_nor(P1)
x = int(P1[0:self.para_len], 16)
return r == ((e + x) % self.n)
def _kg(self, k, Point):
if (k % self.n) == 0:
return '0' * 128
Point = '%s%s' % (Point, '1')
mask_str = '8'
for i in range(self.para_len - 1):
mask_str += '0'
mask = int(mask_str, 16)
Temp = Point
flag = False
for n in range(self.para_len * 4):
if flag:
Temp = self._double_point(Temp)
if (k & mask) != 0:
if flag:
Temp = self._add_point(Temp, Point)
else:
flag = True
Temp = Point
k = k << 1
return self._convert_jacb_to_nor(Temp)
def _double_point(self, Point):
l = len(Point)
len_2 = 2 * self.para_len
if l < self.para_len * 2:
return None
else:
x1 = int(Point[0:self.para_len], 16)
y1 = int(Point[self.para_len:len_2], 16)
if l == len_2:
z1 = 1
else:
z1 = int(Point[len_2:], 16)
T6 = (z1 * z1) % int(self.ecc_table['p'], base=16)
T2 = (y1 * y1) % int(self.ecc_table['p'], base=16)
T3 = (x1 + T6) % int(self.ecc_table['p'], base=16)
T4 = (x1 - T6) % int(self.ecc_table['p'], base=16)
T1 = (T3 * T4) % int(self.ecc_table['p'], base=16)
T3 = (y1 * z1) % int(self.ecc_table['p'], base=16)
T4 = (T2 * 8) % int(self.ecc_table['p'], base=16)
T5 = (x1 * T4) % int(self.ecc_table['p'], base=16)
T1 = (T1 * 3) % int(self.ecc_table['p'], base=16)
T6 = (T6 * T6) % int(self.ecc_table['p'], base=16)
T6 = (self.ecc_a3 * T6) % int(self.ecc_table['p'], base=16)
T1 = (T1 + T6) % int(self.ecc_table['p'], base=16)
z3 = (T3 + T3) % int(self.ecc_table['p'], base=16)
T3 = (T1 * T1) % int(self.ecc_table['p'], base=16)
T2 = (T2 * T4) % int(self.ecc_table['p'], base=16)
x3 = (T3 - T5) % int(self.ecc_table['p'], base=16)
if (T5 % 2) == 1:
T4 = (T5 + ((T5 + int(self.ecc_table['p'], base=16)) >> 1) - T3) % int(self.ecc_table['p'], base=16)
else:
T4 = (T5 + (T5 >> 1) - T3) % int(self.ecc_table['p'], base=16)
T1 = (T1 * T4) % int(self.ecc_table['p'], base=16)
y3 = (T1 - T2) % int(self.ecc_table['p'], base=16)
form = '%%0%dx' % self.para_len
form = form * 3
return form % (x3, y3, z3)
def _add_point(self, P1, P2):
if P1 == '0' * 128:
return '%s%s' % (P2, '1')
if P2 == '0' * 128:
return '%s%s' % (P1, '1')
len_2 = 2 * self.para_len
l1 = len(P1)
l2 = len(P2)
if (l1 < len_2) or (l2 < len_2):
return None
else:
X1 = int(P1[0:self.para_len], 16)
Y1 = int(P1[self.para_len:len_2], 16)
if l1 == len_2:
Z1 = 1
else:
Z1 = int(P1[len_2:], 16)
x2 = int(P2[0:self.para_len], 16)
y2 = int(P2[self.para_len:len_2], 16)
T1 = (Z1 * Z1) % int(self.ecc_table['p'], base=16)
T2 = (y2 * Z1) % int(self.ecc_table['p'], base=16)
T3 = (x2 * T1) % int(self.ecc_table['p'], base=16)
T1 = (T1 * T2) % int(self.ecc_table['p'], base=16)
T2 = (T3 - X1) % int(self.ecc_table['p'], base=16)
T3 = (T3 + X1) % int(self.ecc_table['p'], base=16)
T4 = (T2 * T2) % int(self.ecc_table['p'], base=16)
T1 = (T1 - Y1) % int(self.ecc_table['p'], base=16)
Z3 = (Z1 * T2) % int(self.ecc_table['p'], base=16)
T2 = (T2 * T4) % int(self.ecc_table['p'], base=16)
T3 = (T3 * T4) % int(self.ecc_table['p'], base=16)
T5 = (T1 * T1) % int(self.ecc_table['p'], base=16)
T4 = (X1 * T4) % int(self.ecc_table['p'], base=16)
X3 = (T5 - T3) % int(self.ecc_table['p'], base=16)
T2 = (Y1 * T2) % int(self.ecc_table['p'], base=16)
T3 = (T4 - X3) % int(self.ecc_table['p'], base=16)
T1 = (T1 * T3) % int(self.ecc_table['p'], base=16)
Y3 = (T1 - T2) % int(self.ecc_table['p'], base=16)
form = '%%0%dx' % self.para_len
form = form * 3
return form % (X3, Y3, Z3)
def _convert_jacb_to_nor(self, Point):
len_2 = 2 * self.para_len
x = int(Point[0:self.para_len], 16)
y = int(Point[self.para_len:len_2], 16)
z = int(Point[len_2:], 16)
z_inv = pow(z, int(self.ecc_table['p'], base=16) - 2, int(self.ecc_table['p'], base=16))
z_invSquar = (z_inv * z_inv) % int(self.ecc_table['p'], base=16)
z_invQube = (z_invSquar * z_inv) % int(self.ecc_table['p'], base=16)
x_new = (x * z_invSquar) % int(self.ecc_table['p'], base=16)
y_new = (y * z_invQube) % int(self.ecc_table['p'], base=16)
z_new = (z * z_inv) % int(self.ecc_table['p'], base=16)
if z_new == 1:
form = '%%0%dx' % self.para_len
form = form * 2
return form % (x_new, y_new)
else:
return None
if __name__ == '__main__':
sk = func.random_hex(len(sm2p256v1_ecc_table['n']))
tsm2 = TSM2(sk)
print('pk:%s' %tsm2.pk)
print('pks:%064x'%tsm2.pks)
for i in range(10):
op = input('op: ').strip()
if op == 'sign':
sign(tsm2)
elif op == 'verify':
verify(tsm2)
else:
print("""sign: sign message
verify: verify message""")
啊,这第二题画风就突变,好长的代码,让人失去欲望。但其实呢,大部分都是对sm2的一个实现,其实不用细究。这里我们就直接先提取关键部分,一步一步来啦。
首先最上面的
def sign(tsm2):
data = func.random_hex(len(n))
k1_str = func.random_hex(len(n))
print(tsm2.send_p1(data, k1_str))
backdoor = input('backdoor:').strip()
result = tsm2.output_p1(k1_str, backdoor)
print(result)
def verify(tsm2):
message = input('msg:').strip().encode().strip(b'\x00')
sign = input('sign:').strip().encode().strip(b'\x00')
check = tsm2.verify(sign, message)
if check is True and message == b'Hello, Welcome to ByteCTF2020!':
print(FLAG)
else:
print(check)
俩功能,一个是注册,一个是验证,获取flag的地方就是这个验证,他要求你对message进行一个签名,而message要求是b’Hello, Welcome to ByteCTF2020!’
好的,那我们看看咋样才能给这个message签上名,去找找签名的验证函数。
def verify(self, Sign, data):
r = int(Sign[0:self.para_len], 16)
s = int(Sign[self.para_len:2 * self.para_len], 16)
e = int(data.hex(), 16)
t = (r + s) % self.n
if t == 0:
return 0
P1 = self._kg(s, self.ecc_table['g'])
P2 = self._kg(t, self.pk)
if P1 == P2:
P1 = '%s%s' % (P1, 1)
P1 = self._double_point(P1)
else:
P1 = '%s%s' % (P1, 1)
P1 = self._add_point(P1, P2)
P1 = self._convert_jacb_to_nor(P1)
x = int(P1[0:self.para_len], 16)
return r == ((e + x) % self.n)
这个验证函数有三个输入:r,s,e,然后这里有一个self._kg ,这个其实就是一个椭圆曲线上的一个乘法,所以P1 = s * g,g是椭圆曲线上的一个基点,P2 = t * pk ,代码前头有对pk的定义 self.pk = self._kg(self.sk, ecc_table['g']),所以就是P2 = ((r+s)%n) * sk * g,接下来的操作不难看出,这里就是两个点相加,这里可以print出来看一下输出,是一个点的坐标的十六进制表示的字符串的拼接,x就是这个点的x坐标。最后是一个判断 r == ((e + x) % self.n)
首先e是固定的 b’Hello, Welcome to ByteCTF2020!’。我们能操作的就是r和s了,x是一个算出来的坐标,为了让这个判断成立,我们就需要构造我们的输入r,为了构造r得提前算出P1的x坐标,而P1=P1+P2 = s * g + ((r + s)%n) * sk * g。乍一看我们好像陷入了死锁。这里头怎么又出现了r?
换个思路想想,虽然这里的P1是后来根据我们的输入算出来的,但其实我们也可以先固定这个P1。最后再精心构造一下输入,让他正好算出来是这个P1,
所以假设我们已经知道最后的点P1了,就当他是2g好了,这样我们就可以算出x了,有了x,那么r也就固定下来了,那我们就就只需要构造s让它算出这个P1点了。
我们知道,虽然椭圆曲线的加法和乘法不同于普通的四则运算,但是一些运算法则还是适用的,比如分配律、交换律这些,所以式子:P1=P1+P2 = s * g + ((r + s)%n) * sk * g 可以做一些变形,我们已经知道P1=2g了,外加这条曲线的阶是n(我承认我有赌的成分),所以有
$2*g \equiv s * g + (r + s) * sk * g \pmod n$
$2 \equiv s + (r+s)* sk \pmod n$
$2 \equiv s*(sk+1) + r *sk \pmod n$
$s \equiv (2 -r*sk) *( sk+1)^{-1} \pmod n$
其中r确定了,n确定了,只剩sk了,而sk其实也就是相当于这条椭圆曲线的私钥
这是我们得回过头来看最初的sign函数了
def sign(tsm2):
data = func.random_hex(len(n))
k1_str = func.random_hex(len(n))
print(tsm2.send_p1(data, k1_str))
backdoor = input('backdoor:').strip()
result = tsm2.output_p1(k1_str, backdoor)
print(result)
不能再明显了,backdoor都写给你了,显然是要利用这里来整到sk,
data和k1_str都是不可控的随机数,
然后print了send_p1函数的输出,
def send_p1(self, data, k1_str):
e = int(data, 16)
k1 = int(k1_str, 16)
k1 = k1 % self.n
R1 = self._kg(k1, self.ecc_table['g'])
return '%064x%0128s' % (e, R1)
给的是data和一个R1,R1是k1 * g,是一个曲线上的点,好像没啥用啊,继续看
拿到我们的输入后,程序把k1_str和我们的输入传给了output_p1并给了输出
def output_p1(self, k1_str, r_s2_s3):
r = int(r_s2_s3[0:self.para_len], 16)
s2 = int(r_s2_s3[self.para_len:2 * self.para_len], 16)
s3 = int(r_s2_s3[2 * self.para_len:], 16)
k1 = int(k1_str, 16)
d1 = self.sks
s = (d1 * k1 * s2 + d1 * s3 - r) % self.n
if s == 0 or s == (self.n - r):
return None
return '%064x%064x' % (r, s)
给的是r和s,只要s不等于0,s+r不等于n,
其中我们的输入应该是96字节的,分为三段,代表r,s2,s3,
k1是就是k1_str的整型,程序之前生成的,d1是self.sks,这在代码里头是self.sks = int(func.random_hex(self.para_len), 16)也是一个随机数,但是它和sk跟pks有点关系:self.pks = pow((self.sk + 1) * self.sks, self.n - 2, self.n) % self.n
之所以扯到pks,因为程序一进去他就把这个值给我们了啊
if __name__ == '__main__':
sk = func.random_hex(len(sm2p256v1_ecc_table['n']))
tsm2 = TSM2(sk)
print('pk:%s' %tsm2.pk)
print('pks:%064x'%tsm2.pks)
根据pks的生成式子,其中除了sk和sks我们都知道,
所以我们应该就是要利用这个pks,sks来恢复这个sk,但是怎么获得这个sks 也即 d1 呢,
s = (d1 * k1 * s2 + d1 * s3 - r) % self.n
让s2=0,s3=1,r=0,这样就能得到 s = d1 % n了
显然d1 < n ,故s = d1,并且 d1 + r != n,故能返回。
那么至此,利用链就全了。
解题流程 #
所以这道题的整个解题流程:
- 构造backdoor = 191 * ‘0’ + ‘1’ 来获取sks,
- 利用pks来获取sk,
- 随便在曲线上取一个点,计算x,根据e来固定r
- 计算$s \equiv (2 -r*sk) *( sk+1)^{-1} \pmod n$
- 传入r,s,e,获取flag
exp
from gmssl import func, sm2
from Crypto.Util.number import *
from TSM2 import *
sk = func.random_hex(len(sm2p256v1_ecc_table['n']))
tsm2 = TSM2(sk)
from pwn import *
context.log_level = 'debug'
sh=remote("182.92.215.134","30103")
sh.recvuntil("pk:")
pk =int(sh.recvuntil("\n")[:-1],16)
sh.recvuntil("pks:")
pks=int(sh.recvuntil("\n")[:-1],16)
tsm2.pks=pks
sh.recvuntil("op:")
sh.sendline("sign")
sh.recvuntil("backdoor:")
sh.sendline("0"*191+"1")
sks = int(sh.recvuntil("\n")[:-1],16)
tsm2.sks=sks
tmp = inverse(tsm2.pks,tsm2.n)
tsm2.sk=tmp*inverse(tsm2.sks,tsm2.n)%tsm2.n-1
tsm2.pk = tsm2._kg(tsm2.sk, tsm2.ecc_table['g'])
assert int(tsm2.pk,16)==pk
print(tsm2.sk)
sh.recvuntil("op:")
sh.sendline("verify")
e=bytes_to_long(b'Hello, Welcome to ByteCTF2020!')
b = 2
B = tsm2._kg(b, tsm2.ecc_table['g'])
x = int(B[0:tsm2.para_len], 16)
r = ((e + x) % tsm2.n)
#b = s + (s+r)*sk
#b = s*(1+sk) + r*sk
#b - r*sk
n=0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
print(tsm2.sk,)
s = (b - r*tsm2.sk)*inverse(1+tsm2.sk,n)%n
sign = '%064x%064x' % (r, s)
print(sign)
sh.recvuntil("msg:")
sh.sendline("Hello, Welcome to ByteCTF2020!")
sh.recvuntil("sign:")
sh.sendline(sign)
sh.interactive()
X-NUCA #
weird #
需要前置知识或了解:奇异爱德华曲线
可参考资料:https://learnblockchain.cn/article/1627
#!/usr/bin/env sage
from secret import FLAG
assert FLAG.startswith(b"X-NUCA{") and FLAG.endswith(b"}")
def key_gen(bits):
while True:
p = random_prime(2**bits)
q = random_prime(2**bits)
if p % 4 == 3 and q % 4 == 3:
break
if p < q:
p, q = q, p
N = p * q
while True:
x = getrandbits(bits // 2)
y = getrandbits(bits // 2)
if gcd(x, y) == 1 and (x * y) < (int(sqrt(2 * N)) // 12):
e = randint( int(((p + 1) * (q + 1) * 3 * (p + q) - (p - q) * int(N**0.21)) * y / (x * 3 * (p + q))), int(((p + 1) * (q + 1) * 3 * (p + q) + (p - q) * int(N**0.21)) * y / (x * 3 * (p + q))) )
if gcd(e, (p + 1) * (q + 1)) == 1:
k = inverse_mod(e, (p + 1) * (q + 1))
break
return (N, e, k)
if __name__ == "__main__":
bits = 1024
N, e, _ = key_gen(bits)
pt = (int.from_bytes(FLAG[:32], 'big'), int.from_bytes(FLAG[32:], 'big'))
ct = (0, 1)
d = (((pt[1])**2 - 1) * inverse_mod(((pt[1])**2 + 1) * (pt[0])**2, N)) % N
# 2000 years later...:)
for _ in range(e):
ct = ( int((ct[0] * pt[1] + ct[1] * pt[0]) * inverse_mod(1 + d * ct[0] * pt[0] * ct[1] * pt[1], N) % N), int((ct[1] * pt[1] + d * ct[0] * pt[0]) * inverse_mod(1 - d * ct[0] * pt[0] * ct[1] * pt[1], N) % N) )
f = open("output.txt", "wb")
f.write(str((e, N)).encode() + b'\n')
f.write(str(ct).encode())
f.close()
好的,第一题代码量不多,不错不错(嗯?似曾相识,危。。)首先看看他的功能,加密方式是把flag拆成了左右两份,组成一个数对,然后做了e次的操作,得到一个ct数对。这里的e次操作其实就是一个奇异爱德华曲线的一个乘法操作。(题目名不就是weird么?)所以有了e作为加密的公钥,我们自然就要找私钥d,而私钥d,(我承认我有赌的成分)d=inverse(e,(p+1) * (q+1)),(曾经在一篇paper里看到过一眼,虽然用的并非奇异爱德华曲线)

image-20201102183336623
其中p,q是大数N的一个分解。这里阶的确定不是很严格,但先试试啦。那么要这么试的话就要分解N,那就要看到这个keygen的过程了,这里p,q的生成有一点点小要求,然后就是这个e的生成,为了生成这个e,还特意整了个x,y。最后要求gcd(e, (p+1) * (q+1)),唉,这,感觉我的猜测是对的好叭。到了这里,,这还不像西湖论剑的那一道题嘛 Wake me until May ends。这道题相关的paper提到
如果e满足一定的条件,

image-20201102184915448
那么x,y就会在e/N的连分数上,并且通过x和y可以获得T:p+q的一个近似。

image-20201102184201011
那么回到这道题本身,e的取值
e = randint( int(((p + 1) * (q + 1) * 3 * (p + q) - (p - q) * int(N**0.21)) * y / (x * 3 * (p + q))), int(((p + 1) * (q + 1) * 3 * (p + q) + (p - q) * int(N**0.21)) * y / (x * 3 * (p + q))) )
即$\frac{((p+1) * (q+1) * 3 * (p+q)-(p-q) * N^{0.21}) * y}{x * 3 * (p+q)}<e<\frac{((p+1) * (q+1) * 3 * (p+q)+(p-q) * N^{0.21}) * y}{x * 3 * (p+q)}$
即$ex-(p+1) * (q+1) * y<\frac{|(p-q) * N^{0.21}|}{3(p+q)} * y$
这个范围与paper中给定的$|z|<\frac{|p-q|}{3(p+q)}N^{\frac{1}{4}}y$很类似了,就是paper里头是用的$\phi(N)$,而题目用的是(p+1)(q+1),但问题不大
$ex-(p+1) * (q+1) * y = z$
$ex - y(N + 1 + p + q) = z$
$\frac{ex}{y}-N-p-q-1 = \frac{z}{y}$
$\frac{ex}{y}-N-1 - \frac{z}{y} = p + q$
算一下$\frac{z}{y}$即$\frac{|p-q|}{3(p+q)}N^{0.21}$的大小,约为2048 * 0.21 = 430bit
现在姑且我们把$T = \frac{ex}{y}-N-1$看作是p+q,然后计算$\rho = \frac{T+\sqrt{T^2 -4N}}{2}$,$\rho$作为p的一个近似,其中大约低430bit是不准确的。
这个时候我们就要用到RSA密码系统中用到过的 Factoring with high bits known,

image-20201102192520897
显然这里有430bit的不确定位数是满足这个关系的,于是利用这个算法我们最终能成功的分解出p,q来
然后就能算出这个私钥了。
有了私钥了,这个曲线怎么算呢?
d = (((pt[1])**2 - 1) * inverse_mod(((pt[1])**2 + 1) * (pt[0])**2, N)) % N
# 2000 years later...:)
for _ in range(e):
ct = ( int((ct[0] * pt[1] + ct[1] * pt[0]) * inverse_mod(1 + d * ct[0] * pt[0] * ct[1] * pt[1], N) % N), int((ct[1] * pt[1] + d * ct[0] * pt[0]) * inverse_mod(1 - d * ct[0] * pt[0] * ct[1] * pt[1], N) % N) )
这里有个系数d,首先要计算出这个系数d
这个系数d的计算要利用到题目给的ct,
首先看到扭曲爱德华曲线的定义式

image-20201102193536643
针对这一条曲线的加法公式是

image-20201102193604325
针对这一道题他代码里的那个加法式子,我们会发现,这里相当于是扭曲爱德华曲线的系数a = -d
那么再配上一个坐标(x,y),我们就能计算出系数d了。
其实这里可以做一个思考,这个系数d是有啥用?
我们看到这个源码里这个系数d的生成代码d = (((pt[1])**2 - 1) * inverse_mod(((pt[1])**2 + 1) * (pt[0])**2, N)) % N
这里pt[0],pt[1]是flag明文前后两段的十进制数表示,所以d是由flag明文决定的。
我们再变换上述扭曲爱德华曲线的方程:
$ax^2 + y^2 = 1 + dx^2y^2$
$dx^2y^2+dx^2=y^2 - 1$
$d(x^2(y^2+1))=y^2 - 1$
$d = (y^2-1) * ((y^2+1) * x^2)^{-1}$
可以发现就是这个生成代码的方程式,pt[1]代表y,pt[0]代表x
所以其实这个系数d的作用就是保证flag所代表的点在这条曲线上。
好了,系数d也算出来了,怎么利用私钥来解密呢?
显然不可能直接利用原来里的这个循环去加上这些点,
信安数基中就提到过的重复倍加算法了解一下咯~
解题流程 #
所以这道题的整个解题流程:
- 利用连分数得到x,y(至于怎么确定x,y. 可以根据得到的x,y的bit位数,或者用x,y计算出来的T的bit位数来判断)
- 利用Factoring with high bits known 分解出p,q
- 计算私钥 prikey = inverse(e , (p+1) * (q+1))
- 计算系数$d = (y^2-1) * ((y^2+1) * x^2)^{-1}$
- 利用重复倍加算法做一个乘法计算 mt = d * ct
exp
e,N=(,)
c = continued_fraction(e/N)
for i in range(len(c)):
y=c.numerator(i)
x=c.denominator(i)
if y == 0:
continue
T = e*x//y-N-1
if 1023<(int(T).bit_length()) < 1026: #根据T的bit位数来确定x,y
print(T)
print(x,int(x).bit_length())
print(y,int(y).bit_length())
break
from gmpy2 import * #Factoring with high bits known
_p = (T+iroot(T^2-4*N,int(2))[0])//2
p = int(_p)
n=N
kbits = 430
PR.<x> = PolynomialRing(Zmod(n))
f = x + p
x0 = f.small_roots(X=2^kbits, beta=0.4)[0]
p = p+x0
print("p: ", p)
assert n % p == 0
q = n/int(p)
print("q: ", q)
x,y=(,)
#-d*x*^2 +y^2 = 1+d*x^2*y^2
d = (1-y^2)*inverse_mod(-x^2*y^2-x^2,N)%N #计算系数d
e_inv = inverse_mod(int(e),int((int(p)+1)*(int(q)+1))) #计算私钥prikey
def add(ct,pt): #重复倍加算法的实现
ct = ( int((ct[0] * pt[1] + ct[1] * pt[0]) * inverse_mod(1 + d * ct[0] * pt[0] * ct[1] * pt[1], N) % N), int((ct[1] * pt[1] + d * ct[0] * pt[0]) * inverse_mod(1 - d * ct[0] * pt[0] * ct[1] * pt[1], N) % N) )
return ct
def mul_by_double_adding(ct,n):
pt = (0, 1)
while n > 0:
if n % 2 == 1:
pt = add(ct, pt)
ct = add(ct, ct)
n = n>>1
return pt
(x,y)=mul_by_double_adding((x,y),e_inv) #获取mt,得到flag
from Crypto.Util.number import long_to_bytes
print(long_to_bytes(x)+long_to_bytes(y))
imposter #
Toy_AE.py
import os
from Crypto.Cipher import AES
from Crypto.Util.strxor import strxor
from Crypto.Util.number import long_to_bytes, bytes_to_long
class Toy_AE():
def __init__(self):
self.block_size = 16
self.n_size = self.block_size
self.delta = b'\x00' * self.block_size
self.init_cipher()
def init_cipher(self):
key = os.urandom(16)
self.cipher = AES.new(key = key, mode = AES.MODE_ECB)
def pad(self, m, block_size):
return m if len(m) == block_size else (m + b'\x80' + (b'\x00' * (block_size - 1 - len(m))))
def GF2_mul(self, a, b, n_size):
s = 0
for bit in bin(a)[2:]:
s = s << 1
if bit == '1':
s ^= b
upper = bytes_to_long(long_to_bytes(s)[:-n_size])
lower = bytes_to_long(long_to_bytes(s)[-n_size:])
return upper ^ lower
def encrypt(self, msg):
return self.A_EF(msg)
def decrypt(self, ct, _te):
msg, te = self.A_DF(ct)
return msg if _te == te else None
def A_EF(self, msg):
self.Sigma = b'\x00' * self.n_size
self.L = self.cipher.encrypt(b'ConvenienceFixed')
self.delta = b'DeltaConvenience'
m = len(msg) // self.n_size
m += 1 if (len(msg) % self.n_size) else 0
M_list = [msg[i * self.n_size : (i + 1) * self.n_size] for i in range(m)]
C_list = []
for i in range(0, (m-1)//2):
C1, C2 = self.feistel_enc_2r(M_list[2*i], M_list[2*i +1])
C_list.append(C1)
C_list.append(C2)
self.Sigma = strxor(M_list[2*i +1], self.Sigma)
self.L = long_to_bytes(self.GF2_mul(2, bytes_to_long(self.L), self.n_size))
if m & 1 == 0:
Z = self.cipher.encrypt(strxor(self.L, M_list[-2]))
Cm = strxor(Z[:len(M_list[-1])], M_list[-1])
Cm_1 = strxor(self.cipher.encrypt(strxor(strxor(self.L, self.delta), self.pad(Cm, self.block_size))), M_list[-2])
self.Sigma = strxor(self.Sigma, strxor(Z, self.pad(Cm, self.block_size)))
self.L = strxor(self.L, self.delta)
C_list.append(Cm_1)
C_list.append(Cm)
else:
Cm = strxor(self.cipher.encrypt(self.L)[:len(M_list[-1])], M_list[-1])
self.Sigma = strxor(self.Sigma, self.pad(M_list[-1], self.n_size))
C_list.append(Cm)
if len(M_list[-1]) == self.n_size:
multer = strxor(long_to_bytes(self.GF2_mul(3, bytes_to_long(self.L), self.n_size)), self.delta)
else:
multer = long_to_bytes(self.GF2_mul(3, bytes_to_long(self.L), self.n_size))
TE = self.cipher.encrypt(strxor(self.Sigma, multer))
return b''.join(C_list), TE
def A_DF(self, ct):
self.Sigma = b'\x00' * self.n_size
self.L = self.cipher.encrypt(b'ConvenienceFixed')
self.delta = b'DeltaConvenience'
m = len(ct) // self.n_size
m += 1 if (len(ct) % self.n_size) else 0
C_list = [ct[i * self.n_size : (i + 1) * self.n_size] for i in range(m)]
M_list = []
for i in range(0, (m-1) // 2):
M1, M2 = self.feistel_dec_2r(C_list[2*i], C_list[2*i +1])
self.Sigma = strxor(M2 ,self.Sigma)
self.L = long_to_bytes(self.GF2_mul(2, bytes_to_long(self.L), self.n_size))
M_list.append(M1)
M_list.append(M2)
if m & 1 == 0:
Mm_1 = strxor(self.cipher.encrypt(strxor(strxor(self.L, self.delta), self.pad(C_list[-1], self.block_size))), C_list[-2])
Z = self.cipher.encrypt(strxor(self.L, Mm_1))
Mm = strxor(Z[:len(C_list[-1])], C_list[-1])
self.Sigma = strxor(self.Sigma, strxor(Z, self.pad(C_list[-1], self.block_size)))
self.L = strxor(self.L, self.delta)
M_list.append(Mm_1)
M_list.append(Mm)
else:
Mm = strxor(self.cipher.encrypt(self.L)[:len(C_list[-1])], C_list[-1])
self.Sigma = strxor(self.Sigma, self.pad(Mm, self.block_size))
M_list.append(Mm)
if len(C_list[-1]) == self.n_size:
multer = strxor(long_to_bytes(self.GF2_mul(3, bytes_to_long(self.L), self.n_size)), self.delta)
else:
multer = long_to_bytes(self.GF2_mul(3, bytes_to_long(self.L), self.n_size))
TE = self.cipher.encrypt(strxor(self.Sigma, multer))
return b''.join(M_list), TE
def feistel_enc_2r(self, M1, M2):
C1 = strxor(self.cipher.encrypt(strxor(M1, self.L)), M2)
C2 = strxor(self.cipher.encrypt(strxor(C1, strxor(self.L, self.delta))), M1)
return C1, C2
def feistel_dec_2r(self, C1, C2):
M1 = strxor(self.cipher.encrypt(strxor(C1, strxor(self.L, self.delta))), C2)
M2 = strxor(self.cipher.encrypt(strxor(M1, self.L)), C1)
return M1, M2
task.py
#!/usr/bin/env python3
import os
import random
import string
from hashlib import sha256
from Toy_AE import Toy_AE
from secret import FLAG
def proof_of_work():
random.seed(os.urandom(8))
proof = b''.join([random.choice(string.ascii_letters + string.digits).encode() for _ in range(20)])
digest = sha256(proof).hexdigest().encode()
print("sha256(XXXX+%s) == %s" % (proof[4:],digest))
print("Give me XXXX:")
x = input().encode()
return False if len(x) != 4 or sha256(x + proof[4:]).hexdigest().encode() != digest else True
def pack(uid, uname, token, cmd, appendix):
r = b''
r += b'Uid=%d\xff' % uid
r += b'UserName=%s\xff' % uname
r += b'T=%s\xff' % token
r += b'Cmd=%s\xff' % cmd
r += appendix
return r
def unpack(r):
data = r.split(b"\xff")
uid, uname, token, cmd, appendix = int(data[0][4:]), data[1][9:], data[2][2:], data[3][4:], data[4]
return (uid, uname, token, cmd, appendix)
def apply_ticket():
uid = int(input("Set up your user id:")[:5])
uname = input("Your username:").encode("ascii")[:16]
if uname == b"Administrator":
print("Sorry, preserved username.")
return
token = sha256(uname).hexdigest()[:max(8, uid % 16)].encode("ascii")
cmd = input("Your command:").encode("ascii")[:16]
if cmd == b"Give_Me_Flag":
print("Not allowed!")
return
appendix = input("Any Appendix?").encode("ascii")[:16]
msg = pack(uid, uname, token, cmd, appendix)
ct, te = ae.encrypt(msg)
print("Your ticket:%s" % ct.hex())
print("With my Auth:%s" % te.hex())
def check_ticket():
ct = bytes.fromhex(input("Ticket:"))
te = bytes.fromhex(input("Auth:"))
msg = ae.decrypt(ct, te)
assert msg
uid, uname, token, cmd, appendix = unpack(msg)
if uname == b"Administrator" and cmd == b"Give_Me_Flag":
print(FLAG)
exit(0)
else:
print("Nothing happend.")
def menu():
print("Menu:")
print("[1] Apply Ticket")
print("[2] Check Ticket")
print("[3] Exit")
op = int(input("Your option:"))
assert op in range(1, 4)
if op == 1:
apply_ticket()
elif op == 2:
check_ticket()
else:
print("Bye!")
exit(0)
if __name__ == "__main__":
ae = Toy_AE()
if not proof_of_work():
exit(-1)
for _ in range(4):
try:
menu()
except:
exit(-1)
可恶,果然是这样吗。。不只代码长,甚至附件都有俩。害,慢慢啃咯。。。先不管这个加密的具体是啥,来看看功能是啥叭。程序有俩功能,提供ticket,和检查ticket,获取flag的点在检查ticket,
def decrypt(self, ct, _te):
msg, te = self.A_DF(ct)
return msg if _te == te else None
msg = ae.decrypt(ct, te)
assert msg
uid, uname, token, cmd, appendix = unpack(msg)
if uname == b"Administrator" and cmd == b"Give_Me_Flag":
print(FLAG)
要求你的这个ticket代表的信息是,用户名是Administrator,要执行的命令是Give_Me_Flag,并且还要提供这个ticket的签名Auth来保证他的合法性。
再来看看这个提供ticket有啥,
def apply_ticket():
uid = int(input("Set up your user id:")[:5])
uname = input("Your username:").encode("ascii")[:16]
if uname == b"Administrator":
print("Sorry, preserved username.")
#return
token = sha256(uname).hexdigest()[:max(8, uid % 16)].encode("ascii")
cmd = input("Your command:").encode("ascii")[:16]
if cmd == b"Give_Me_Flag":
print("Not allowed!")
#return
appendix = input("Any Appendix?").encode("ascii")[:16]
msg = pack(uid, uname, token, cmd, appendix)
他要求你提供,uid,用户名,cmd,和额外的可选择的信息。其中,用户名不能等于Administrator,cmd不能等于Give_Me_Flag。(不然这题直接就没了。)然后他会生成一个你的用户名的sha256的摘要,至于存多少长读进你的message呢,由你的uid来决定。
token = sha256(uname).hexdigest()[:max(8, uid % 16)].encode("ascii")
然后一些限制是,除了uid最大为5位数字之外,其余输入最多只能16个字符,并且每个字符的ascii都得在0-128之间(由decode(‘ascii’)限制)。(不然你要是输入\xff,这题也直接就没了)
所以题目意思很明确,你要伪造密文,并且还要能够构造对应的签名来通过合法性验证。让他解密信息后用户名为Administrator,cmd为Give_Me_Flag。然后由于对输入做的诸多限制,(甚至一次连接只能交互4次,除去一次来获取flag,只能交互三次,下一次连接就生成新的Toy_AE对象,生成新的key了)导致漏洞点大概率不会出现在这个task文件中,,那就要找这个Toy_AE算法的洞了。(啊,好长,不想看)
一点点啃叭,先大致随便看看,然后我们有目的性的先来看看生成Auth的过程。(单独拎出来会清晰些)
self.Sigma = b'\x00' * self.n_size
self.Sigma = strxor(M_list[2*i +1], self.Sigma)
if 组数为偶数:
Z = self.cipher.encrypt(strxor(self.L, M_list[-2]))
Cm = strxor(Z[:len(M_list[-1])], M_list[-1])
self.Sigma = strxor(self.Sigma, strxor(Z, self.pad(Cm, self.block_size)))
else:
self.Sigma = strxor(self.Sigma, self.pad(M_list[-1], self.n_size))
TE = self.cipher.encrypt(strxor(self.Sigma, multer))
TE = self.cipher.encrypt(strxor(self.Sigma, multer))
可以看到,如果组数为偶数,就会多生成一个Z,而且生成的密文方式也会比较麻烦,那么我们就先利用那个附加信息来控制组数,尽量避免这个麻烦的东西。
这样子的话Sigma第2块、第4块明文、填充后的第5块明文的异或,然后和multer
if len(M_list[-1]) == self.n_size:
multer = strxor(long_to_bytes(self.GF2_mul(3, bytes_to_long(self.L), self.n_size)), self.delta)
else:
multer = long_to_bytes(self.GF2_mul(3, bytes_to_long(self.L), self.n_size))
(multer和L有关,不可知,那就不管了)异或,最后AES加密,返回密文。
由于AES的key也不可知,所以我们想要拿到Auth,没别的方法了。只能在传明文获取Auth时,让我们的msg的第二块和第四块和第五块和真正的能拿到FLAG的msg的明文保持一致了。
这里一个做法就是,本地跑这个程序,把那些麻烦的PoW啥的去去掉,一些限制(比如用户名不能是Administrator)也去去掉,然后打印一些方便我们审计的信息,(当然,熟用那种自带debug编译器的大佬可以忽略,IDLE选手还是比较喜欢print debug大法)
那就是怎么伪造密文了。
先看看密文的生成
C1, C2 = self.feistel_enc_2r(M_list[2*i], M_list[2*i +1])
def feistel_enc_2r(self, M1, M2):
C1 = strxor(self.cipher.encrypt(strxor(M1, self.L)), M2)
C2 = strxor(self.cipher.encrypt(strxor(C1, strxor(self.L, self.delta))), M1)
return C1, C2
我们把明文和密文看成16字节一块,两块一组,两块明文对自己这组生成的密文有影响,但每组明文间的加密是独立的。也就是第一组(第一二块)明文不影响第二组(第三四块)明文生成的第二块密文。
那么,如果我们的uid是1,用户名是Administrator,cmd是Give_Me_Flag,不加信息,
(本地起这个程序,把用户名和cmd的限制给取消掉,然后打印一下M_list)
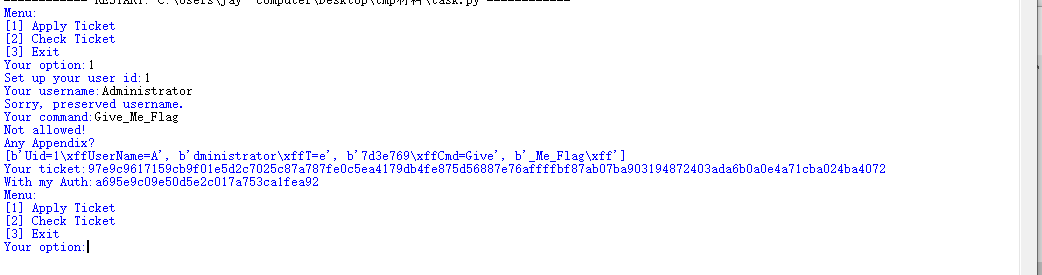
image-20201102204318891
我们会生成4块明文,[b'Uid=1\xffUserName=A', b'dministrator\xffT=e', b'7d3e769\xffCmd=Give', b'_Me_Flag\xff']
前面说了,为了让生成的Auth便于计算,我们要加入附加信息(Appendix)来控制明文组数。
但这里先看看M_list叭,如果我们想要得到Auth,那么我们就得保证我们构造的用户名和cmd在不等于限定值的情况下,M_list的第二组和第四组与用户名为Administrator和cmd为Give_Me_Flag时的M_list的相应分组相同。
这样子看过去,对于我们目前得到的这个M_list是很好构造的,由于Administrator的A在第一组,那么我们注册Bdministrator;由于Give_Me_Flag的Give在第三组,那么我们注册give_Me_Flag就好了。然后加一加Appendix控制下组数。但是注意到第二组最后一位是sha256的首位,而我们要是动了用户名,这个值大概率也有变,所以我们还得控制这个用户名的首位,可能不能是B,我们就在ascii 为0到128之间找一个字符*,让*dministrator的sha256的首位为e就可以了。经过测试,字符‘P’就是一个合适的值
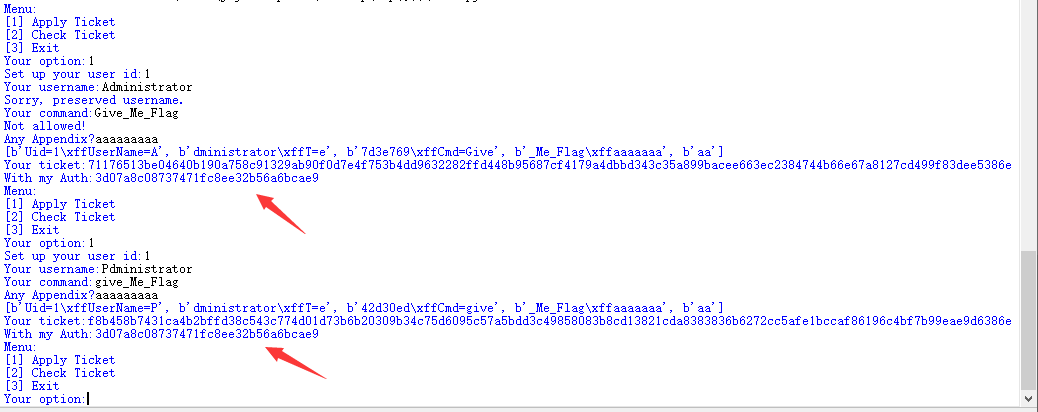
image-20201102234733848
看,上面是目标Auth,下面是我们伪造的用户名和cmd获取的Auth,他们是一致的。所以Auth这一关过了。那就只剩下密文的伪造了。
对于第一组,是由uid和用户名决定的。其中uid不用伪造,问题不大,但是用户名的密文咋办,我们用户名不能等于Administrator,但是又要搞到的Administrator的密文。
这里用到的第一技巧就是,增加uid的长度,反正uid最后模16了,我们控制uid长度为5,用户名为Administratorr(多了一个r),这样子对照一下,
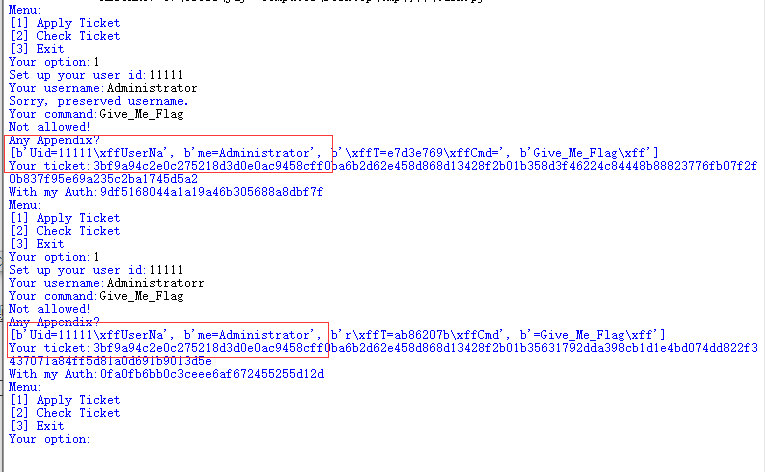
image-20201102235135632
可以发现,多出来的那个r正好被挤到第三组去了,这样子我们的用户名既没有等于Administrator,但是又获得了前两块属于Administrator的msg的密文。
ok。一半的工作完成。
第二组,由于uid那么构造了,那么第二组明文就是这样子的,b'r\xffT=ab86207b\xffCmd', b'=Give_Me_Flag\xff由hash和cmd和组成(这里只是测试,附加信息就先不加了)。
这里我们要的是cmd=Give_Me_Flag的密文,怎么伪造cmd呢?我们不能改变任何一个字符,不然由于AES的存在,密文整个就不一样了。但是输入的cmd又不能等于Give_Me_Flag。这里我们还是用前面的方法,由于这里分组加密的特性,我们把cmd顶到第二块的末尾,大概就是让第二组的第二块明文是这样子,
'Cmd=Give_Me_Flag'
刚好16个字节,然后我们的命令就可以改成Give_Me_Flagg,多的g到第五块去了,咱们就不用管了。至于怎么顶,这里就要利用uid了,在uid长度仍然保持为5的情况下,进行加减,控制hash的长度为12就好了,11111%16 = 7,那就用11116,
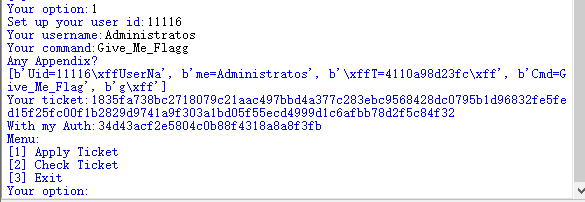
image-20201218133935540
可以看到这样\xffT=4110a98d23fc\xff刚好占满了第二组第一块的16字节,'Cmd=Give_Me_Flag占了另一块。而我们输入的cmd命令是Give_Me_Flagg,是能过验证的。这样交互,让他加密,就能得到明文:b'\xffT=4110a98d23fc\xff', b'Cmd=Give_Me_Flag'生成的密文了。但是这里还有个问题,hash由用户名控制,用户名为Administrator的12位hash是e7d3e769f3f5,然而我们又不能注册用户为Administrator,那一个想法就是,碰撞,找一个由可见字符串组成的13位字符串(Administrator的长度),sha256后前12位为e7d3e769f3f5就可以了。然而这显然不现实,12位是96bit,有这算力,比特币不是随便挖?所以这题有解的一个原因就是,这个系统并没有验证用户名的hash,所以你随便整个用户名就好(我们这里就用的Administratos)。
但是新问题产生了,Auth的获取怎么办?现在我们的uid=11116,我们来看看用户名为Administrator,cmd为Give_Me_Flag的情况

image-20201103001239680
想要得到Auth,就得构造同样的第二块、第四块明文,第二块明文还好说,用户名我们多打一个字符就能绕过检查了,而这个字符也会被顶到第三块,对Auth没有影响,并且我们也可以uid相应的减1,让第四块密文不受到影响。但是第四块的明文本身就不好操作啊,这里要是也多打一个字符绕过的话,第五组就多了一个字符,这样产生的Auth就完全对不上了。
所以要把证获取到正确的Auth,我们需要第二块,第四块,第五块分别为:b'me=Administrator', b'Cmd=Give_Me_Flag', b'\xff'
这里我的做法是,缩短uid为两位长,构造用户名为:me=Administrator,控制uid%16为8,构造cmd为Cmd=Give_Me_Flag
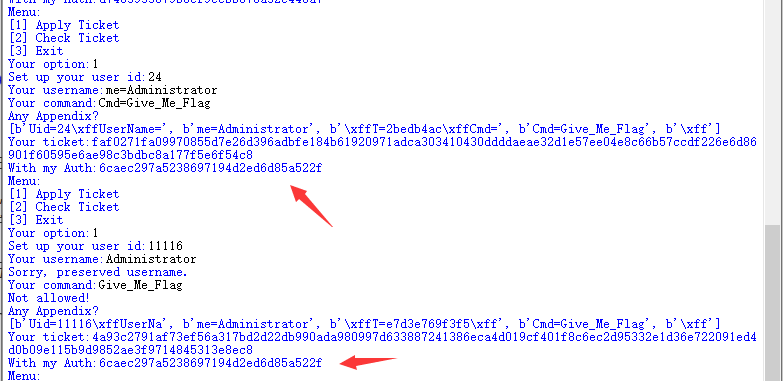
image-20201103002724699
可以看到是完全一致的。如果此时打印出来了C_list的话,也会发现,此时这两组产生的C_list的最后一组也是一致的,因为我们这里M_list的到数两组是一致的。
解题流程 #
所以这道题的整个解题流程:(交互可以直接手撸)
- uid:24,name:me=Administrator,cmd:Cmd=Give_Me_Flag 获取Auth和第三段密文
- uid:11116,name:me=Administratorr,后面随意 获取第一段密文
- uid:11116,name:Administratos,cmd:Give_Me_Flagg 获取第二段密文
- 发送Auth和三段密文的拼接,获取flag
exp
from pwn import *
sh=remote("123.57.4.93","45216")
from pwnlib.util.iters import mbruteforce
from hashlib import sha256
context.log_level = 'debug'
def proof_of_work(sh):
sh.recvuntil("XXXX+b\'")
suffix = sh.recvuntil("\'").decode("utf8")[:-1]
log.success(suffix)
sh.recvuntil("== b\'")
cipher = sh.recvuntil("\'").decode("utf8")[:-1]
print(suffix)
print(cipher)
proof = mbruteforce(lambda x: sha256((x + suffix).encode()).hexdigest() == cipher, string.ascii_letters + string.digits, length=4, method='fixed')
sh.sendlineafter("Give me XXXX:", proof)
proof_of_work(sh)
sh.recvuntil("option:")
sh.sendline('1')
sh.recvuntil("id:")
sh.sendline('24')
sh.recvuntil("name:")
sh.sendline("me=Administrator")
sh.recvuntil("and:")
sh.sendline("Cmd=Give_Me_Flag")
sh.recvuntil("?")
sh.sendline("")
sh.recvuntil("ket:")
ticket=sh.recvuntil("\n")[:-1]
sh.recvuntil("Auth:")
Auth=sh.recvuntil("\n")[:-1]
sh.recvuntil("option:")
sh.sendline("1")
sh.recvuntil("id:")
sh.sendline("65548")
sh.recvuntil("name:")
sh.sendline("Administratorr")
sh.recvuntil("and:")
sh.sendline("Give_Me_Flagg")
sh.recvuntil("?")
sh.sendline("")
sh.recvuntil("ket:")
ticket1=sh.recvuntil("\n")[:-1]
sh.recvuntil("option:")
sh.sendline('1')
sh.recvuntil("id:")
sh.sendline('65548')
sh.recvuntil("name:")
sh.sendline("Administratos")
sh.recvuntil("and:")
sh.sendline("Give_Me_Flagg")
sh.recvuntil("?")
sh.sendline("")
sh.recvuntil("ket:")
ticket2=sh.recvuntil("\n")[:-1]
sh.recvuntil("option:")
sh.sendline('2')
sh.recvuntil("Ticket:")
sh.sendline(ticket1[:64]+ticket2[64:64*2]+ticket[-2:])
sh.recvuntil("Auth:")
sh.sendline(Auth)
sh.interactive()
2021 AntCTF x D^3CTF #
babyLattice #
题目分析 #
这道题的题目如下
from collections import namedtuple
PublicKey = namedtuple('PublicKey', ['n', 'b'])
SecretKey = namedtuple('SecretKey', ['p', 'q', 'A'])
def gen_key():
p = random_prime(2^512, lbound=2^511)
q = random_prime(2^512, lbound=2^511)
n = p * q
a11, a12, a21 = [random_prime(2^100) for _ in range(3)]
a22 = random_prime(2^100)
while a11 * a22 == a12 * a21:
a22 = random_prime(2^100)
A = Matrix(ZZ, [[a11, a12], [a21, a22]])
a1 = crt([a11, a21], [p, q])
a2 = crt([a12, a22], [p, q])
b = a1 * inverse_mod(a2, n) % n
PK = PublicKey(n, b)
SK = SecretKey(p, q, A)
return (PK, SK)
def encrypt(m, pk):
assert 0 < m < 2^400
r = randint(0, 2^400-1)
c = (pk.b*m + r) % pk.n
return c
def decrypt(c, sk):
a2 = crt([sk.A[0,1], sk.A[1,1]], [sk.p, sk.q])
s1 = a2 * c % sk.p
s2 = a2 * c % sk.q
m, r = sk.A.solve_right(vector([s1, s2]))
return m
def test(pk, sk, num=3):
for _ in range(num):
m = randint(0, 2^400-1)
c = encrypt(m, pk)
mm = decrypt(c, sk)
assert m == mm
if __name__ == '__main__':
from hashlib import sha256
from secret import m, FLAG
assert FLAG == 'd3ctf' % sha256(int(m).to_bytes(50, 'big')).hexdigest()
PK, SK = gen_key()
test(PK, SK)
c = encrypt(m, PK)
print(f"PK = {PK}")
print(f"c = {c}")
我们重点看看加密函数
也就是
这样就可以通过LLL算法还原出m了
EXP #
from hashlib import sha256
n = 69804507328197961654128697510310109608046244030437362639637009184945533884294737870524186521509776189989451383438084507903660182212556466321058025788319193059894825570785105388123718921480698851551024108844782091117408753782599961943040695892323702361910107399806150571836786642746371968124465646209366215361
b = 65473938578022920848984901484624361251869406821863616908777213906525858437236185832214198627510663632409869363143982594947164139220013904654196960829350642413348771918422220404777505345053202159200378935309593802916875681436442734667249049535670986673774487031873808527230023029662915806344014429627710399196
c = 64666354938466194052720591810783769030566504653409465121173331362654665231573809234913985758725048071311571549777481776826624728742086174609897160897118750243192791021577348181130302572185911750797457793921069473730039225991755755340927506766395262125949939309337338656431876690470938261261164556850871338570
A = Matrix(ZZ,[[1,0,b],[0,2^400,c],[0,0,n]])
A = A.LLL()
m = int(A[0][0])
flag = 'd3ctf' % sha256(int(m).to_bytes(50, 'big')).hexdigest()
print(flag)
simpleGroup #
题目分析 #
这道题的题目如下
from random import randint
from secret import FLAG
# A gift for key recovery in challenge [babyLattice]
n = 69804507328197961654128697510310109608046244030437362639637009184945533884294737870524186521509776189989451383438084507903660182212556466321058025788319193059894825570785105388123718921480698851551024108844782091117408753782599961943040695892323702361910107399806150571836786642746371968124465646209366215361
y = 12064801545723347322936991186738560311049061235541031580807549422258814170771738262264930441670708308259694588963224372530498305648578520552038029773849342206125074212912788823834152785756697757209804475031974445963691941515756901268376267360542656449669715367587909233618109269372332127072063171947435639328
e = 1928983487
M = int.from_bytes(FLAG, 'big')
C = []
while M != 0:
m = M % e
M //= e
r = randint(0, n-1)
c = power_mod(y, m, n) * power_mod(r, e, n)
C.append(c % n)
print(f"C = {C}")
通过注释我们可以大概猜测babyLattice本来是需要分解n的,但是因为被非预期了所以又出了这道题目
那么我们回到babyLattice题目里面,我们知道的参数实际上只有b,c,n,分解n应该和b有关,通过阅读b的生成代码我们可以得到
我们展开后两个式子
也就是
两边相乘得到
展开并变形得到
也就是
由于
所以我们同样可以用LLL还原出目标向量,然后使用factor进行分解(a11,a12,a21,a22它们都是素数)
当分解完毕后,通过猜测它们对应的值来分解n,即
得到p,q后,我们回来看题目里面的加密,其会对FLAG进行取模并分段加密余数,其中c的生成公式如下
r是随机生成的数字,而e可以被分解为e1和e2两个素数,这两个素数又分别是p-1和q-1的因子
那么我们可以得到
通过遍历j并判断得到的c'是不是为模p的e1次剩余,我们就可以得到m模e1的值
同样我们也可以用q得到m模e2的值,然后使用中国剩余定理即可还原m并最终得到flag
EXP #
n = 69804507328197961654128697510310109608046244030437362639637009184945533884294737870524186521509776189989451383438084507903660182212556466321058025788319193059894825570785105388123718921480698851551024108844782091117408753782599961943040695892323702361910107399806150571836786642746371968124465646209366215361
b = 65473938578022920848984901484624361251869406821863616908777213906525858437236185832214198627510663632409869363143982594947164139220013904654196960829350642413348771918422220404777505345053202159200378935309593802916875681436442734667249049535670986673774487031873808527230023029662915806344014429627710399196
c = 64666354938466194052720591810783769030566504653409465121173331362654665231573809234913985758725048071311571549777481776826624728742086174609897160897118750243192791021577348181130302572185911750797457793921069473730039225991755755340927506766395262125949939309337338656431876690470938261261164556850871338570
A = Matrix(ZZ,[[1,0,b^2],[0,1,b],[0,0,n]])
A = A.LLL()
x1 = -A[0][0]
x3 = A[0][2]
print(factor(x1))
print(factor(x3))
a12 = 1018979931854255696816714991181
a22 = 1151291153120610849180830073509
a11 = 1017199123798810531137951821909
a21 = 207806651167586080788016046729
print(gcd(b * a12 - a11,n))
print(gcd(b * a22 - a21,n))
p = 7669036313101194621345265255994200133006921565596653797956940811601516306410232120057637504305295677357422367597831138570269733177579895994340511712373309
q = 9102122415165681824420871673621781250311822805618731863628192549895693024247220594372897360668046264863189831887100676431439200352775676467952192600956629
assert(p * q == n)
#!/usr/bin/env python
from Crypto.Util.number import *
import gmpy2
p = 7669036313101194621345265255994200133006921565596653797956940811601516306410232120057637504305295677357422367597831138570269733177579895994340511712373309
q = 9102122415165681824420871673621781250311822805618731863628192549895693024247220594372897360668046264863189831887100676431439200352775676467952192600956629
n = 69804507328197961654128697510310109608046244030437362639637009184945533884294737870524186521509776189989451383438084507903660182212556466321058025788319193059894825570785105388123718921480698851551024108844782091117408753782599961943040695892323702361910107399806150571836786642746371968124465646209366215361
y = 12064801545723347322936991186738560311049061235541031580807549422258814170771738262264930441670708308259694588963224372530498305648578520552038029773849342206125074212912788823834152785756697757209804475031974445963691941515756901268376267360542656449669715367587909233618109269372332127072063171947435639328
e = 1928983487
e1 = 36493
e2 = 52859
def GCRT(mi, ai):
assert (isinstance(mi, list) and isinstance(ai, list))
curm, cura = mi[0], ai[0]
for (m, a) in zip(mi[1:], ai[1:]):
d = gmpy2.gcd(curm, m)
c = a - cura
assert (c % d == 0)
K = c // d * gmpy2.invert(curm // d, m // d)
cura += curm * K
curm = curm * m // d
cura %= curm
return (cura % curm, curm)
def check(d,p,n):
if((p - 1) % n == 0):
return pow(d,(p - 1) // n,p) == 1
else:
k = gmpy2.gcd(n, p - 1)
return pow(d,(p - 1) // k,p) == 1
def getM(c,e,p):
for i in range(2,e):
tmpc = (c * gmpy2.invert(pow(y,i,p),p)) % p
if check(tmpc,p,e):
return i
exit(0)
C = [63173987757788284988620600191109581820396865828379773315280703314093571300861961873159324234626635582246705378908610341772657840682572386153960342976445563045427986000105931341168525422286612417662391801508953619857648844420751306271090777865836201978470895906780036112804110135446130976275516908136806153488, 9763526786754236516067080717710975805995955013877681492195771779269768465872108434027813610978940562101906769209984501196515248675767910499405415921162131390513502065270491854965819776080041506584540996447044249409209699608342257964093713589580983775580171905489797513718769578177025063630080394722500351718, 37602000735227732258462226884765737048138920479521815995321941033382094711120810035265327876995207117707635304728511052367297062940325564085193593024741832905771507189762521426736369667607865137900432117426385504101413622851293642219573920971637080154905579082646915297543490131171875075081464735374022745371, 1072671768043618032698040622345664216689606325179075270470875647188092538287671951027561894188700732117175202207361845034630743422559130952899064461493359903596018309221581071025635286144053941851624510600383725195476917014535032481197737938329722082022363122585603600777143850326268988298415885565240343957, 27796821408982345007197248748277202310092789604135169328103109167649193262824176309353412519763498156841477483757818317945381469765077400076181689745139555466187324921460327576193198145058918081061285618767976454153221256648341316332169223400180283361166887912012807743326710962143011946929516083281306203120, 27578857139265869760149251280906035333246393024444009493717159606257881466594628022512140403127178174789296810502616834123420723261733024810610501421455454191654733275226507268803879479462533730695515454997186867769363797096196096976825300792616487723840475500246639213793315097434400920355043141319680299224, 29771574667682104634602808909981269404867338382394257360936831559517858873826664867201410081659799334286847985842898792091629138292008512383903137248343194156307703071975381090326280520578349920827357328925184297610245746674712939135025013001878893129144027068837197196517160934998930493581708256039240833145, 33576194603243117173665354646070700520263517823066685882273435337247665798346350495639466826097821472152582124503891668755684596123245873216775681469053052037610568862670212856073776960384038120245095140019195900547005026888186973915360493993404372991791346105083429461661784366706770467146420310246467262823, 5843375768465467361166168452576092245582688894123491517095586796557653258335684018047406320846455642101431751502161722135934408574660609773328141061123577914919960794180555848119813522996120885320995386856042271846703291295871836092712205058173403525430851695443361660808933971009396237274706384697230238104, 61258574367240969784057122450219123953816453759807167817741267194076389100252707986788076240792732730306129067314036402554937862139293741371969020708475839483175856346263848768229357814022084723576192520349994310793246498385086373753553311071932502861084141758640546428958475211765697766922596613007928849964, 13558124437758868592198924133563305430225927636261069774349770018130041045454468021737709434182703704611453555980636131119350668691330635012675418568518296882257236341035371057355328669188453984172750580977924222375208440790994249194313841200024395796760938258751149376135149958855550611392962977597279393428]
m = 0
for c in C[::-1]:
cp = c % p
cq = c % q
m1 = getM(cp,e1,p)
m2 = getM(cq,e2,q)
mm,lcm = GCRT([e1,e2],[m1,m2])
print("Get mm: " + hex(mm))
m *= e
m += mm
flag = long_to_bytes(m)
print(flag)
EasyCurve #
题目分析 #
这道题目的主要部分如下
import socketserver
from Crypto.PublicKey import RSA
from Crypto.Util.number import getPrime , bytes_to_long
from Curve import MyCurve
from hashlib import sha256
import os
import string
import random
import signal
from secret import flag
BIT = 2048
p = 9688074905643914060390149833064012354277254244638141162997888145741631958242340092013958501673928921327767591959476890238698855704376126231923819603296257
class Task(socketserver.BaseRequestHandler):
def proof_of_work(self):
random.seed(os.urandom(8))
proof = ''.join([random.choice(string.ascii_letters+string.digits) for _ in range(20)])
_hexdigest = sha256(proof.encode()).hexdigest()
self.send(f"sha256(XXXX+{proof[4:]}) == {_hexdigest}".encode())
self.send(b'Give me XXXX: ')
x = self.recv()
if len(x) != 4 or sha256(x+proof[4:].encode()).hexdigest() != _hexdigest:
self.send('wrong')
return False
return True
def recv(self):
data = self.request.recv(1024)
return data.strip()
def send(self, msg, newline=True):
if isinstance(msg , bytes):
msg += b'\n'
else:
msg += '\n'
msg = msg.encode()
self.request.sendall(msg)
def key_gen(self , bit):
key = RSA.generate(bit)
return key
def ot(self , point):
x , y = point
random.seed(os.urandom(8))
key = self.key_gen(BIT)
self.send('n = ' + str(key.n))
self.send('e = ' + str(key.e))
x0 = random.randint(1 , key.n)
x1 = random.randint(1 , key.n)
self.send("x0 = " + str(x0))
self.send("x1 = " + str(x1))
self.send("v = ")
v = int(self.recv())
m0_ = (x + pow(v - x0, key.d, key.n)) % key.n
m1_ = (y + pow(v - x1, key.d, key.n)) % key.n
self.send("m0_ = " + str(m0_))
self.send("m1_ = " + str(m1_))
def handle(self):
signal.alarm(180)
if not self.proof_of_work():
return 0
e = bytes_to_long(os.urandom(32))
u = random.randint(1 , p)
D = random.randint(1 , p)
curve = MyCurve(p , D , u)
self.send('p = ' + str(p))
self.send('D = ' + str(D))
for i in range(3):
G = curve.getPoint()
self.ot(G)
P = curve.mul(e , G)
self.ot(P)
self.send("do you know my e?")
guess = int(self.recv())
if guess == e:
self.send("oh no!")
self.send(flag)
return 0
else:
self.send("Ha, I know you can't get it.")
class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
pass
if __name__ == "__main__":
HOST, PORT = '0.0.0.0', 10000
server = ForkedServer((HOST, PORT), Task)
server.allow_reuse_address = True
server.serve_forever()
其使用了一个随机生成参数的MyCurve并生成了随机的e,给我们三次交互的机会,每次交互会随机生成点G和点P并使用OT将这两个点的信息传递给我们,点P是e倍的点G,当我们给服务器正确的e的时候我们可以得到flag
这其实就是一个离散对数问题,我们首先关注服务器的参数,MyCurve所使用的p是512比特的,而OT中RSA的n是2048比特的,这样生成的点的x和y乘起来也没有n的大。那么可以参考2020hackergame的
不经意传输中的攻击方式来同时获取点的x和y坐标
之后便是如何通过点G和点P来获取e了,我们可以注意到p-1是光滑的
sage: factor(p-1)
2^21 * 3^10 * 7^4 * 11 * 13^2 * 17 * 19 * 29 * 31 * 37 * 43^3 * 47 * 71 * 83 * 89 * 97 * 223 * 293 * 587 * 631 * 709 * 761 * 1327 * 1433 * 1733 * 1889 * 2503 * 3121 * 6043 * 6301 * 49523 * 98429 * 140683 * 205589 * 1277369 * 1635649 * 5062909 * 45698189 * 67111151 * 226584089 * 342469397
那么我们可以通过
Pohlig-Hellman algorithm来解决离散对数问题并最终得到flag
EXP #
exp有概率成功,如果报错或者答案错误多跑几次即可
#!/usr/bin/env python
import string, gmpy2
from hashlib import sha256
from pwn import *
context.log_level = "debug"
dic = string.ascii_letters + string.digits
def solvePow(prefix,h):
for a1 in dic:
for a2 in dic:
for a3 in dic:
for a4 in dic:
x = a1 + a2 + a3 + a4
proof = x + prefix.decode("utf-8")
_hexdigest = sha256(proof.encode()).hexdigest()
if _hexdigest == h.decode("utf-8"):
return x
def getData():
r.recvuntil("n = ")
n = int(r.recvuntil("\n", drop = True))
r.recvuntil("e = ")
e = int(r.recvuntil("\n", drop = True))
r.recvuntil("x0 = ")
x0 = int(r.recvuntil("\n", drop = True))
r.recvuntil("x1 = ")
x1 = int(r.recvuntil("\n", drop = True))
offset = 2 << 1024
offset_e = int(pow(offset, e, n))
v = ((offset_e * x0 - x1) * gmpy2.invert(offset_e - 1, n)) % n
r.sendlineafter("v = ",str(v))
r.recvuntil("m0_ = ")
m0 = int(r.recvuntil("\n", drop = True))
r.recvuntil("m1_ = ")
m1 = int(r.recvuntil("\n", drop = True))
m = (m0 * offset - m1) % n
x = m // offset + 1
y = x * offset - m
return x,y
r = remote("47.100.50.252",10000)
r.recvuntil("sha256(XXXX+")
prefix = r.recvuntil(") == ", drop = True)
h = r.recvuntil("\n", drop = True)
result = solvePow(prefix,h)
r.sendlineafter("Give me XXXX: \n",result)
r.recvuntil("p = ")
r.recvuntil("\n", drop = True)
r.recvuntil("D = ")
D = int(r.recvuntil("\n", drop = True))
Gx,Gy = getData()
Px,Py = getData()
with open("data.txt","wb") as f:
f.write(str(D).encode() + b"\n")
f.write(str(Gx).encode() + b"\n")
f.write(str(Gy).encode() + b"\n")
f.write(str(Px).encode() + b"\n")
f.write(str(Py).encode() + b"\n")
s = process(argv=["sage", "exp.sage"])
e = int(s.recv())
s.close()
r.sendline(str(e))
r.interactive()
# exp.sage
load("Curve.sage")
p = 9688074905643914060390149833064012354277254244638141162997888145741631958242340092013958501673928921327767591959476890238698855704376126231923819603296257
F = GF(p)
fac = [2^21,3^10,7^4,11,13^2,17,19,29,31,37,43^3,47,71,83,89,97,223,293,587,631,709,761,1327,1433,1733,1889,2503,3121,6043,6301,49523,98429,140683,205589,1277369,1635649,5062909,45698189,67111151,226584089,342469397]
def bsgs(g, y, p):
m = int(ceil(sqrt(p - 1)))
S = {}
point = (u,0)
for i in range(m):
point = curve.add(point,g)
pointg = point[0] << 800 | point[1]
S[pointg] = i
gs = curve.mul(m,g)
for i in range(m):
pointy = y[0] << 800 | y[1]
if pointy in S:
return S[pointy] - i * m + 1
y = curve.add(y,gs)
return None
def Pohlig_Hellman(G,P):
ea = []
na = []
for i in range(len(fac)):
c = fac[i]
n = (p - 1) // c
gi = curve.mul(n, G)
yi = curve.mul(n, P)
ei = bsgs(gi,yi,c)
ea.append(ei%c)
na.append(c)
ee = crt(ea,na)
return ee
data = open("data.txt","rb").read().decode("utf-8")
data = data.split("\n")
D = int(data[0])
Gx = int(data[1])
Gy = int(data[2])
Px = int(data[3])
Py = int(data[4])
G = (F(Gx),F(Gy))
P = (F(Px),F(Py))
u2 = (Gx ^ 2 - D * Gy ^ 2)
u2 = F(u2)
u = int(u2.sqrt())
curve = MyCurve(p , D , u)
e = Pohlig_Hellman(G,P)
e %= p - 1
print(e)
AliceWantFlag #
题目分析 #
这道题目分为server端和Alice端,其中server端的代码如下
from elgamal import elgamal
import socketserver
from prikey import server_prikey , AlicePasswd
from pubkey import Alice_pubkey
from secret import Alice_flag , ctfer_flag
import random
import signal
from os import urandom
from Crypto.Util.number import long_to_bytes , bytes_to_long
from Crypto.Cipher import AES
MENU = "1. signup 2.signin"
XOR = lambda s1,s2 :bytes([x1^x2 for x1 , x2 in zip(s1,s2)])
def pad(m):
m += bytes([16 - len(m) % 16] * (16 - len(m) % 16))
return m
def unpad(m):
padlen = m[-1]
for i in range(1 , padlen + 1):
if m[-i] != m[-1]:
return b''
return m[:-m[-1]]
class server(socketserver.BaseRequestHandler):
def setup(self):
self.pubkey = {}
self.passwd = {}
self.prikey = elgamal(server_prikey)
self.pubkey[b'Alice'] = elgamal(Alice_pubkey)
self.passwd[b'Alice'] = AlicePasswd
def _recv(self):
data = self.request.recv(1024)
return data.strip()
def _send(self, msg, newline=True):
if isinstance(msg , bytes):
msg += b'\n'
else:
msg += '\n'
msg = msg.encode()
self.request.sendall(msg)
def enc_send(self, msg , usrid , enc_key = b''):
if enc_key == b'':
pubenc = self.pubkey[usrid]
y1 , y2 = pubenc.encrypt(bytes_to_long(msg))
self._send(str(y1) + ', ' + str(y2))
else:
assert len(enc_key) == 16
aes = AES.new(enc_key , AES.MODE_ECB)
self._send(aes.encrypt(pad(msg)))
def dec_recv(self, enc_key = b''):
msg = self._recv()
if enc_key == b'':
c = [int(i) for i in msg.split(b', ')]
m = self.prikey.decrypt(c)
print(long_to_bytes(m))
return long_to_bytes(m)
else:
assert len(enc_key) == 16
aes = AES.new(enc_key , AES.MODE_ECB)
return unpad(aes.decrypt(msg))
def signup(self):
if len(self.passwd) > 5:
self._send('sorry, the number of users is out of limit')
return 0
self._send('please give me your name')
userid = self._recv()
if len(userid) > 20:
self._send('your id can\'t be too long')
return 0
elif userid in self.passwd:
self._send('the name has been used')
return 0
else:
self._send('please give me your passwd(encrypted)')
userpasswd = self.dec_recv()
if len(userpasswd) > 11:
self._send('your password can\'t be too long')
return 0
else:
self.passwd[userid] = userpasswd
self._send('please give me your publickey')
userpubkey = self._recv()
try:
userpubkey = [int(i) for i in userpubkey[1:-1].split(', ')]
except:
self._send('publickey format error')
self.passwd.pop(userid)
return 0
self.pubkey[userid] = elgamal(userpubkey)
self._send('sign up success')
return 1
def signin(self):
self._send('please give me your name')
userid = self._recv()
if userid not in self.passwd:
self._send('sorry the userid is not existed')
return 0
while 1:
random.seed(urandom(8))
r = random.getrandbits(8 * 11)
self._send('please give me your passwd(encrypted and xored by r)')
self._send(str(r))
userdata = self.dec_recv()
if bytes_to_long(userdata) == r ^ bytes_to_long(self.passwd[userid]):
self._send('signin success')
break
else:
self._send('password error')
endkey = urandom(5)
key = userdata + endkey
self._send('now let\'s communicate with this key')
self.enc_send(endkey , userid)
return userid , key
def handle(self):
signal.alarm(240)
key = b''
userid = ''
while 1:
self._send(MENU)
choice = self._recv()
if choice == b'1':
self.signup()
elif choice == b'2':
temp = self.signin()
if temp != 0:
userid , key = temp
break
else:
self._send('error')
msg = self.dec_recv(enc_key = key)
if msg == b'I am a ctfer.Please give me flag':
self.enc_send(b'ok, your flag is here ' + ctfer_flag , userid , enc_key= key)
elif msg == b'I am Alice, Please give me true flag' and userid == b'Alice':
self.enc_send(b'Hi Alice, your flag is ' + Alice_flag , userid , enc_key= key)
return 0
def finish(self):
self.request.close()
class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
pass
if __name__ == "__main__":
HOST, PORT = '0.0.0.0', 10001
server = ForkedServer((HOST, PORT), server)
server.allow_reuse_address = True
server.serve_forever()
Alice端的代码如下
import socket
from elgamal import elgamal
from pubkey import server_pubkey
from prikey import Alice_prikey , AlicePasswd
from Crypto.Util.number import long_to_bytes , bytes_to_long
from Crypto.Cipher import AES
import socketserver , signal
def pad(m):
m += bytes([16 - len(m) % 16] * (16 - len(m) % 16))
return m
def unpad(m):
return m[:-m[-1]]
class Alice:
def __init__(self , ip , port):
self.pridec = elgamal(Alice_prikey)
self.pubenc = elgamal(server_pubkey)
self.s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
self.s.connect((ip, port))
def _recv(self):
data = self.s.recv(1024)
return data.strip()
def _send(self, msg):
if isinstance(msg , str):
msg = msg.encode()
self.s.send(msg)
def enc_send(self, msg , enc_key = b''):
if enc_key == b'':
y1 , y2 = self.pubenc.encrypt(bytes_to_long(msg))
self._send(str(y1) + ', ' + str(y2))
else:
assert len(enc_key) == 16
aes = AES.new(enc_key , AES.MODE_ECB)
self._send(aes.encrypt(pad(msg)))
def dec_recv(self, enc_key = b''):
msg = self._recv()
if enc_key == b'':
c = [int(i) for i in msg.split(b', ')]
m = self.pridec.decrypt(c)
return long_to_bytes(m)
else:
assert len(enc_key) == 16
aes = AES.new(enc_key , AES.MODE_ECB)
return unpad(aes.decrypt(msg))
def main(self):
firstmsg = self._recv()
if firstmsg != b'1. signup 2.signin':
return 0
self._send('2')
self._recv()
self._send('Alice')
self._recv()
r = int(self._recv())
userdata = long_to_bytes(bytes_to_long(AlicePasswd) ^ r)
self.enc_send(userdata)
self._recv()
self._recv()
endkey = self.dec_recv()
key = userdata + endkey
self.enc_send(b'I am a ctfer.Please give me flag' , enc_key = key)
return self.dec_recv(enc_key = key)
class Task(socketserver.BaseRequestHandler):
def _recv(self):
data = self.request.recv(1024)
return data.strip()
def _send(self, msg, newline=True):
if isinstance(msg , bytes):
msg += b'\n'
else:
msg += '\n'
msg = msg.encode()
self.request.sendall(msg)
def handle(self):
signal.alarm(60)
self._send('Hello, I am Alice, can you tell me the address of the server?\nIn return, I will give you the ctf_flag')
try:
addr = self._recv()
ip, port = [x.strip() for x in addr.split(b':')]
port = int(port)
except:
ip, port = '0.0.0.0', 10001
a = Alice(ip , port)
msg = a.main()
self._send(b'Thanks, here is your flag')
self._send(msg)
class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
pass
if __name__ == "__main__":
HOST, PORT = '0.0.0.0', 10003
server = ForkedServer((HOST, PORT), Task)
server.allow_reuse_address = True
server.serve_forever()
server和Alice的密钥生成和使用都和elgamal算法一致,这里不再阐述
服务端的大概逻辑如下
U: User
S: Server
UserPasswd = UserPublicKey
Sign Up:
S -> U : 'please give me your name'
U -> S : userid
S : assert len(userid) <= 20 and userid not in passwd
S -> U : 'please give me your passwd(encrypted)'
U -> S : c = elgamal.enc(UserPasswd,ServerPublicKey)
S : userpasswd = elgamal.dec(c,ServerPrivateKey
S : assert len(userpasswd) <= 11
S : passwd[userid] = userpasswd
S -> U : 'sign up success'
Sign In:
S -> U : 'please give me your name'
U -> S : userid
S : assert userid in passwd
S -> U : 'please give me your passwd(encrypted and xored by r)'
S -> U : r = random.getrandbits(8 * 11)
U -> S : c = elgamal.enc(UserPasswd ^ r,ServerPublicKey)
S : assert elgamal.dec(c,ServerPrivateKey) == passwd[userid] ^ r
S : key = userdata + endkey, userdata = passwd[userid] ^ r, endkey = urandom(5)
S -> U : 'now let\'s communicate with this key'
S -> U : k = elgamal.enc(key,UserPasswd)
U -> S : m = AES.enc(key,msg)
S : dm = AES.dec(key,m)
S : if dm == 'I am a ctfer.Please give me flag':
S -> U : r1 = AES.enc(key,ctfer_flag)
S : if dm == 'I am Alice, Please give me true flag' and userid == 'Alice'
S -> U : r2 = AES.enc(key,Alice_flag)
大概理解下来就是一个利用elgamal进行密钥交换然后加密通信的逻辑
由于这里我们需要以Alice的身份登陆并使用交换的AES通信密钥进行密文的加密,所以我们需要知道AlicePasswd和key
这道题目中由于也有Alice端的服务,所以我们可以伪装成服务端来和Alice端进行通信,也就是进行中间人攻击
首先来看看如何获得AlicePasswd,观察Alice端的如下代码
def main(self):
firstmsg = self._recv()
if firstmsg != b'1. signup 2.signin':
return 0
self._send('2')
self._recv()
self._send('Alice')
self._recv()
r = int(self._recv())
userdata = long_to_bytes(bytes_to_long(AlicePasswd) ^ r)
self.enc_send(userdata)
self._recv()
self._recv()
endkey = self.dec_recv()
key = userdata + endkey
self.enc_send(b'I am a ctfer.Please give me flag' , enc_key = key)
return self.dec_recv(enc_key = key)
def dec_recv(self, enc_key = b''):
msg = self._recv()
if enc_key == b'':
c = [int(i) for i in msg.split(b', ')]
m = self.pridec.decrypt(c)
return long_to_bytes(m)
else:
assert len(enc_key) == 16
aes = AES.new(enc_key , AES.MODE_ECB)
return unpad(aes.decrypt(msg))
由于endkey长度为5,而key的长度是16,那么可以自然推断出userdata的长度为11
但是如果我们控制r使得userdata的第一个字节异或为了\x00,那么userdata的长度就变成了10,如果endkey的长度不变,再使用userdata + endkey作为AES的key,那么会通不过assert len(enc_key) == 16,即连接会断开
这样我们可以通过单字节爆破AlicePasswd的值使得key的长度从16变成15,这样就能获得AlicePasswd的第一个字节,然后重复该过程便可以获得AlicePasswd(每爆破出一个字节,在爆破下一个字节的时候将endkey的长度变长一位即可连续爆破)
PS:实际上的操作过程中AlicePasswd的最后一个字节爆破不出来,我们使用服务端的Sign In功能来爆破最后一个字节即可
在拿到了AlicePasswd之后,我们便可以伪造成Alice登陆服务端,但是由于endkey是使用AlicePublicKey来进行加密的,所以我们还需要拿到endkey的值才能获得AES的key并进行任意文本加解密
前面我们提过,endkey长度为5,但是实际上elgamal的p是512比特的,也就是说endkey远比p小
如果我们将elgamal加密后的endkey的y2乘以一个倍数k,那么elgamal解密后的endkey就会变大k倍,这个值如果特别大,则userdata + endkey就也会变大,这样便会通不过assert len(enc_key) == 16,即连接会断开
那么我们就可以通过遍历k并查看连接是否断开来得到endkey的大致范围,然后通过控制r让userdata的长度变小来使得我们的k可以不断变大,进而将endkey的取值范围不断缩小来得到endkey
最后我们便可以进行任意文本加解密来获取flag
EXP #
爆破AlicePasswd的脚本(除了最后一个字节)
#!/usr/bin/env python
from elgamal import elgamal
from os import urandom
from Crypto.Util.number import *
from pwn import *
from time import *
import random
#context.log_level = 'debug'
Alice_pubkey = (10701440058624032601015137538928332495339102166449611910023158626004456760436930147541475696463030881833656888220652983522600176918743749340172660134163173, 1564399668655593150166497641453625075939863931648697579307, 7485644640971189066076867813504769638089749022750276585841131549227880841063823940682209946365975810625990180843110530957715179877761206203179636693608929, 10399272689500457356753299445284422908920074489727610618928888372268024186959263604721857776550008093778901180936272708522371781846820901338928077050396521)
pubenc = elgamal(Alice_pubkey)
def enc(msg):
y1 , y2 = pubenc.encrypt(bytes_to_long(msg))
return [y1,y2]
def attackAlice(rr,m):
try:
middle_shell = listen(8888)
alice_shell = remote("47.100.0.15",10003)
alice_shell.recvuntil(b"Hello, I am Alice, can you tell me the address of the server?\nIn return, I will give you the ctf_flag\n")
alice_shell.sendline("xxxx:8888") # xxxx -> your vps's ip
middle_shell.sendline(b'1. signup 2.signin')
middle_shell.recv()
middle_shell.sendline(b'please give me your name')
middle_shell.recv()
middle_shell.sendline(b'please give me your passwd(encrypted and xored by r)')
middle_shell.sendline(str(rr))
middle_shell.recv()
middle_shell.sendline(b'signin success')
middle_shell.sendline(b'now let\'s communicate with this key')
middle_shell.sendline(str(m[0]) + ', ' + str(m[1]))
sleep(0.3)
result = middle_shell.recv()
if result != b"":
middle_shell.close()
alice_shell.close()
return True
except:
if middle_shell:
middle_shell.close()
if alice_shell:
alice_shell.close()
return False
known_pwd = b""
# 0x35343764643163636333xx
for i in range(11):
for r in range(0,256):
rr = ((bytes_to_long(known_pwd) << 8) + r) << ((11 - i - 1) * 8)
print("try:" + hex(rr))
msg = b"A" * (5 + i)
c = enc(msg)
if not attackAlice(rr,c):
known_pwd += long_to_bytes(r)
print(known_pwd.hex())
break
爆破AlicePasswd的最后一个字节的脚本
#!/usr/bin/env python
from elgamal import elgamal
from os import urandom
from Crypto.Util.number import *
from pwn import *
from time import *
import random
#context.log_level = 'debug'
dic = "0123456789abced"
server_pubkey = (8299337325013713958100496214277076548352330213422739951900206795659160881192662528217175848727001874097369338994314737585158671248737646741717255122339339, 1168114014665994438995759247944846107956060291607878556427, 6500863983405565947154848535503122330952083500341721347265599161478330537510643776384164499549064061675517930495094496645911948535824156417648599603482256, 1567838365897620258270310904624368598290758028096181970817619626094906443214320401208038763050717813632540079799097716376430981907783174222429828480377116)
pubenc = elgamal(server_pubkey)
known_pwd = "547dd1ccc3"
server_shell = remote("47.100.0.15",10001)
server_shell.sendlineafter("\n","2")
server_shell.recvuntil("please give me your name\n")
server_shell.sendline("Alice")
for c in dic:
server_shell.recvuntil("please give me your passwd(encrypted and xored by r)\n")
rr = int(server_shell.recvline())
pwd = bytes_to_long((known_pwd + c).encode())
prefix = long_to_bytes(pwd ^ rr)
assert(len(prefix) == 11)
y1 , y2 = pubenc.encrypt(pwd ^ rr)
server_shell.sendline(str(y1) + ', ' + str(y2))
result = server_shell.recv()
if b"success" in result:
print(known_pwd + c)
break
server_shell.interactive()
获取endkey并进行中间人攻击的脚本
#!/usr/bin/env python
from pwn import *
from Crypto.Util.number import *
from Crypto.Cipher import AES
from elgamal import elgamal
#context.log_level = "debug"
pwd = "547dd1ccc38".encode()
pwd = bytes_to_long(pwd)
server_pubkey = (8299337325013713958100496214277076548352330213422739951900206795659160881192662528217175848727001874097369338994314737585158671248737646741717255122339339, 1168114014665994438995759247944846107956060291607878556427, 6500863983405565947154848535503122330952083500341721347265599161478330537510643776384164499549064061675517930495094496645911948535824156417648599603482256, 1567838365897620258270310904624368598290758028096181970817619626094906443214320401208038763050717813632540079799097716376430981907783174222429828480377116)
pubenc = elgamal(server_pubkey)
p = 10701440058624032601015137538928332495339102166449611910023158626004456760436930147541475696463030881833656888220652983522600176918743749340172660134163173
def pad(m):
m += bytes([16 - len(m) % 16] * (16 - len(m) % 16))
return m
def unpad(m):
padlen = m[-1]
for i in range(1 , padlen + 1):
if m[-i] != m[-1]:
return b''
return m[:-m[-1]]
def oracle(m,n,p):
y1 = m[0]
y2 = m[1]
y2 = (y2 * n) % p
return [y1,y2]
def combineKey(m,rr):
for i in range(3):
sleep(0.3)
try:
middle_shell = listen(8888)
alice_shell = remote("47.100.0.15",10003)
alice_shell.recvuntil(b"Hello, I am Alice, can you tell me the address of the server?\nIn return, I will give you the ctf_flag\n")
alice_shell.sendline("xxxx:8888") # xxxx -> your vps's ip
middle_shell.sendline(b'1. signup 2.signin')
middle_shell.recv()
middle_shell.sendline(b'please give me your name')
middle_shell.recv()
middle_shell.sendline(b'please give me your passwd(encrypted and xored by r)')
middle_shell.sendline(str(rr))
middle_shell.recv()
middle_shell.sendline(b'signin success')
middle_shell.sendline(b'now let\'s communicate with this key')
middle_shell.sendline(str(m[0]) + ', ' + str(m[1]))
sleep(0.5)
result = middle_shell.recv()
print(result)
if result != b"":
middle_shell.close()
alice_shell.close()
return True
except:
if middle_shell:
middle_shell.close()
if alice_shell:
alice_shell.close()
return False
server_shell = remote("47.100.0.15",10001)
server_shell.sendlineafter("\n","2")
server_shell.recvuntil("please give me your name\n")
server_shell.sendline("Alice")
server_shell.recvuntil("please give me your passwd(encrypted and xored by r)\n")
rr = int(server_shell.recvline())
prefix = long_to_bytes(pwd ^ rr)
assert(len(prefix) == 11)
y1 , y2 = pubenc.encrypt(pwd ^ rr)
server_shell.sendline(str(y1) + ', ' + str(y2))
server_shell.recvuntil("now let's communicate with this key\n")
y1,y2 = [int(i) for i in server_shell.recvuntil("\n", drop = True).decode("utf-8").split(", ")]
print(y1,y2)
success("Get communicate key:" + str(y1) + "," + str(y2))
l = 0
h = 2**40
idx = 0
prefix_length = 0
bound = 2**40
count = 0
flag = False
for _ in range(11):
if flag:
break
binary_ptr = 0x80
diff = binary_ptr // 2
assert_arr = [-1] * 256
for i in range(10):
count += 1
if binary_ptr != 0 and assert_arr[binary_ptr-1] ^ assert_arr[binary_ptr] == 1:
prefix_length += 1
l = bound // multiple
h = bound // (multiple - 1)
idx = multiple - 1
print(hex(l),hex(h),count)
bound *= 0x100
if abs(h - l) < 2:
flag = True
break
if binary_ptr != 255 and assert_arr[binary_ptr] ^ assert_arr[binary_ptr+1] == 1:
prefix_length += 1
l = bound // (multiple + 1)
h = bound // multiple
idx = multiple
print(hex(l),hex(h),count)
bound *= 0x100
if abs(h - l) < 2:
flag = True
break
rr = bytes_to_long(long_to_bytes(pwd)[:prefix_length]) * 2**(8*(11 - prefix_length))
multiple = idx * 0x100 + binary_ptr
m = oracle([y1,y2],multiple,p)
if combineKey(m,rr):
if binary_ptr == 255:
prefix_length += 1
h = bound // (multiple + 1)
idx = multiple + 1
print(hex(l),hex(h),count)
bound *= 0x100
if abs(h - l) < 2:
exit(0)
break
assert_arr[binary_ptr] = 0
binary_ptr += diff
diff //= 2
else:
assert_arr[binary_ptr] = 1
binary_ptr -= diff
diff //= 2
context.log_level = "debug"
endkey = long_to_bytes(h)
key = prefix + endkey
success("get key:" + key.hex())
data = b'I am Alice, Please give me true flag'
cipher = AES.new(key , AES.MODE_ECB)
data = cipher.encrypt(pad(data))
server_shell.sendline(data)
msg = server_shell.recvuntil("\n",drop = True)
print(cipher.decrypt(msg))
参考 #
https://github.com/USTC-Hackergame/hackergame2020-writeups/blob/master/official/不经意传输/README.md
https://ctf-wiki.org/crypto/asymmetric/discrete-log/discrete-log/#pohlig-hellman-algorithm
莲城杯 经典随机数Yusa的密码学课堂——MT19937 #
又是这个系列的题
有三个文件都已经上传至 github仓库里了
虽然考点还是MT19937伪随机数,但是这个是在C++下写的;之前发过关于这类题的文章,但今天去看写地太烂了,处刑一下,完全没有搞懂嘛
https://4xwi11.github.io/posts/2d82e8aa/
解决上次的一个问题

并非不是需要624个数,而是需要凑足32*624位,也就是64*312位
所以如果是纯python的话,这道题应该秒出,但问题是C++;试了下就算给相同的种子,但生成的随机数序列也是不同的,算法略有出路应该
代码不长,贴一下
import subprocess
import os
import random
import hashlib
subprocess.run(["g++", "random.cpp", "-o", "random", "-std=c++11"],check=True)
proc = subprocess.Popen(["./random"],stdin=subprocess.PIPE,stdout=subprocess.PIPE)
# out, err = proc.communicate(str(int(os.urandom(8).hex(),16)).encode() + b"\n")
out, err = proc.communicate(str(16063322316592949072).encode() + b"\n")
data = out.strip().split()
flag = random.randint(0,len(data))
FLAG = b'DASCTF{'+hashlib.md5(data.pop(flag)).hexdigest().encode()+b'}'
data = list(map(int,data))
with open("outputs_%d.txt"%flag,"w") as f:
f.write(str(data))
#include <cinttypes>
#include <iostream>
#include <random>
int main() {
uint64_t seed;
std::cin >> seed;
std::mt19937_64 rng(seed);
for (int i = 0; i < 1000; ++i) {
std::cout << rng() << '\n';
}
return 0;
}
好了,开始讲这道题的思路

这张图出来的有点早(doge)
先看到最后,这个flag在文件名中,就是pop出来的伪随机数,是374
with open("outputs_%d.txt"%flag,"w") as f:
f.write(str(data))
但可惜根据pop,虽然我们知道data,但是是删除了原第374位的data
需要通过其余373+625个数字求得这位
显然根据之前的mt19937predictor,和前373位(这个上面刚解释过)以及后面的625位,是完全可以获得的,然后再得到第374个,拿捏
可是试过了不行,用了恢复的方法也不行;然后就想是不是C++的问题
所以接下来的搜索思路就如上图所示,搜索关键词c++和mt19937以及predict,当然一般都返回32位的结果,所以加上64;原题到手
改下jo本就有
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
from mt19937_64 import mt19937_64
import hashlib
res = [15224110489171130169, 1487925206988459477, 13480727356180709371, 9868256411224235526, 6217804851957837168, 16087170136679200450, 10701512125563075829, 13839719157982856576, 17686330611486610733, 8009416170371519873, 5970669226517080452, 11269217943220347675, 10679128876184101302, 18426494309927575430, 2766502893811979226, 2252796059596895410, 9426444128738501522, 11240845202238046967, 10773508588111955623, 1557877671900503598, 10687052904024584487, 1329391365184628727, 7924797549450027243, 8535390433774276870, 3764662861183967374, 2246153524896469598, 2609915142724872757, 10658867097171399935, 5527882090828515536, 16980061916688614551, 369781677154768879, 16440083865102214341, 6215352314823709568, 7140216739817729337, 12081906179615786779, 6478685619216942062, 9619055260791569210, 1716773987678792695, 5781591055396867866, 10236249441362668669, 4314491602044042424, 9076763991771914801, 1019089589927696539, 12783145303781447438, 1784730974216681496, 10724359773647505800, 9412346711065789784, 12397469196070741661, 844871001521064632, 13554026965219580112, 4176961812003667679, 6038315983316303141, 3991176913179867636, 7277063843827680934, 6593392965255927508, 7279379575539700793, 7049180319367268844, 2484858153711481256, 9662542622219218463, 15645318283754749515, 7848634356524747132, 6328770785215004957, 14031726511284712999, 10754197358715401067, 14877197602427408826, 1961981170873480756, 15043831614315156076, 2703733192099380300, 5573267746680488476, 2588678833804270160, 16641900531805836732, 14485077651674686804, 17908682116840210486, 12129346423391778925, 449323128784312129, 2912052724053440605, 3725415122737515057, 12106075465626310804, 7844624661111246261, 4336975117722586651, 6133486737560458810, 4285708852412482387, 17320873594107961221, 18154223303204659281, 9782280317517313987, 7359883602982876716, 8302270318241074541, 2854871868457850608, 4260073478828444220, 12464166743488435720, 11545300218414290638, 15943917616147672791, 17684529969128042573, 11970487736986863722, 4279463896104155311, 6452386490939306659, 14951002814044492267, 3924373366113113482, 17675004214657643053, 10514060213491578166, 5083735479763236962, 8237048074291002693, 178024658423258428, 16217384550361068797, 6823885072554733775, 14640293890442769000, 11118102735797335929, 17687811899187265346, 12324758265458544032, 13305186849598403772, 2061361200506122451, 4473679754720240444, 15364566282531130774, 10360818283823976655, 17220043518084908852, 9386042935320331823, 10932555460714805145, 14286030551222176204, 5513294049464657489, 9643782458509542843, 2950842616838528179, 16153550634060410597, 10622243240110203305, 1642938210383117587, 16348894212565750617, 17802404752703029833, 16933001622790235864, 13021337058260052257, 17301160463217879931, 4914154622730751038, 3649150598994385675, 17138640742876844054, 6723182378145435688, 15799828338293133322, 994720218982390675, 10557290726979603665, 17714019041621996643, 13997848863450584994, 11077445104717373075, 2834856239311065051, 11214787995926447582, 4068838695613829268, 3318186966385494373, 10984597623033520694, 5515414919887778777, 7222755179917827587, 16315875605087375576, 1416504086864662519, 9102186857132686420, 10069600536464217172, 6582524821522410340, 15369756932292150641, 17542632941176957329, 6114252881995050176, 2055179652476914195, 16405356136326356060, 14344232008993353644, 7357227068527869292, 14444189009256502503, 474793712655159763, 7277957134452370555, 10136894698074936516, 16493593438906441399, 965972604086413481, 7698637742708237198, 14701582675687476239, 8687372870093533304, 8617910444450923438, 9198266698377902297, 17663341461584809487, 9416311128064169723, 15527623086766043739, 17634355913948865190, 18230067880107976101, 14647282067432289184, 2666571742016867486, 35944775638564196, 13202068495097382260, 9200881323819852309, 4609224846213708248, 18385087669463550574, 10907111573029619720, 3677665280613822779, 7175067246924173873, 11557554314793111361, 16459269098754836930, 15069426419433415372, 3478942161672373533, 1475410410806061275, 3951913608914307936, 9031385401155758661, 3487921219891556908, 14331439795449455643, 18005194978393081205, 17499558816128213969, 10013697255070423725, 5656707783041395866, 8245156232824114523, 5484825401635850101, 18276565390397117490, 9806016278660472039, 6246223529755503034, 16322603114524844950, 13512386112109766619, 4292997062471342719, 5482339873158479974, 12153068771020641259, 18134128714075076811, 3921582705345984456, 17990063870067007106, 11893303237020637674, 584000375933180982, 6837860293438757570, 8668590806728300645, 10930322698482157784, 3456591010166906694, 8479176164660731035, 1378913458575066776, 11867206231852016448, 11155774780214677606, 912636353429261442, 17286540002553508524, 2342876557589322779, 8472494814582696749, 1649463863153987977, 6639761134830802698, 17749792536888103944, 6682611142368155837, 8961391229631067960, 16808632462882238050, 12764361808843833740, 3494650449008997672, 13464542575897195823, 424905026997643448, 6949880018570988189, 4352171970901905656, 7585977087659274602, 9963800442502096068, 11967585318365690786, 1330206767381639342, 8961211309807685961, 12822173985081341335, 4508173450257371182, 5828692808060501375, 7437728885533218362, 11924888116770741814, 2012177013990519412, 6499123439580002081, 13085942749253543550, 12967954280047984193, 401135611301783756, 3748733649551258520, 3742761952933734129, 7180568637515019340, 8490711531714639868, 1461899626173313114, 15357996742461975417, 14566908736002266815, 18368411028248688780, 2276282088146233438, 13500510232438577028, 5042075854511929699, 6430943865985944461, 4611615451136427723, 16501718400150227301, 12689032035555572221, 15097412730296922717, 3917094315801026114, 2738852375492418821, 16365967597393176630, 15062401340541737624, 14638139755970734808, 17586333334851266372, 17319918915751492871, 11845068873340136881, 1459249680175909613, 7472745361441793631, 1812384806700690960, 8855007047564417997, 2163690632469050637, 1883216720349119806, 17992478845633263598, 4665099551190282678, 11678011021345341884, 14187013186800119116, 14052476937717753457, 14759086517840933234, 5009467219504023390, 4622766434224603629, 14306333222661486071, 3858064603145888263, 5480134807934395111, 4123024571389908319, 4857052736700414325, 16243980005326285458, 3632766067814039781, 710008964341406746, 5363960844618609694, 14114730195035015808, 16428297947621094568, 7700974694607772814, 16793381582485703202, 13948380472150916306, 14326581900789123198, 4228968193234651142, 11100829582225662535, 17495023276082596914, 8634787791698085471, 6145765583313197421, 16788430897014030178, 11435692770927277650, 18065086017618584565, 11769581244567937207, 13278489473631493919, 8019460929320111149, 5693618935245539106, 3634811597737081216, 12859793273631344580, 11287301384880619752, 18394782048366983264, 7421132200962846807, 4084540937457316264, 13113874388366064762, 8131358879566215449, 18127561595469413694, 8734770900165404534, 17424357262393464853, 10097252723684474013, 13657127819021358228, 15053911843606144518, 7213762907694003185, 9201850376693257882, 1152437224214832892, 14749316667846084768, 13945981875336291326, 17205113012613835387, 17208682023098019636, 16837244935188768969, 1562887481274292099, 4817091557053520861, 12788128805488570720, 12001115261194850091, 4003771944165077120, 2234627252583081046, 9648802166794733209, 2217782127954322431, 8813298931273365931, 8055654179906713224, 11975882101529377223, 3484952924454621378, 9405558259370977621, 10465136460923462995, 10114188036427722127, 3137605056932583175, 6052770256806365938, 13216705997825407019, 9321595432845767721, 7404913363748792748, 3104222247113734338, 7884841839505302190, 10282600744363227974, 10560288140635802837, 345714099277926722, 14827599919753819919, 15348137034782912153, 117188792560235416, 721765732450403598, 13484574492955662118, 4088456941206683834, 7978001820773876706, 3458688202384309003, 7297824025882346112, 8366103370544240004, 14726906913567147182, 17890463553725848943, 11056300998383817861, 12172218496062907284, 5614991059403362329, 94695117905761066, 13704554396573869457, 6942259376738368761, 3724125954238286617, 605665642089906206, 4440357634786283101, 9312356527281045726, 18433419763563298916, 5537070555239228268, 13655980751929630271, 11097112793938372280, 7029091093125181071, 15682558111863651240, 9864810256451039130, 5940287037201593945, 7230113292992804565, 1262540470928338201, 9310270195989362278, 5911475921308141211, 5943394248414176333, 2467090711423218798, 14834589937967531968, 2112412521637455955, 4483762121635552341, 9203453183301626690, 12517949271946792756, 11765267562048769695, 2130431799048385018, 1021118212271885825, 4527525148317213493, 2666979235110630076, 11385323575772505236, 1957143482002768471, 6653869545594001852, 9403787903811093312, 8793399260966849492, 9134129177479686128, 5344549741728076030, 3785525706196259331, 4098427281238979781, 14780185570363454606, 15022528285132147394, 4415868057026363350, 11652850077219368760, 6599101465769202844, 2324709069440458374, 2328030874184313596, 5375810578496425005, 3324352283736262699, 8961596405474061089, 17555556238164816340, 1217170962166712882, 12300833475020082526, 5755163501951705747, 17673007557139716816, 5400175616849815689, 16424974447872124521, 3528336073009821153, 5677112613986511204, 11681713850480599971, 17889123911033641068, 13398947136669841280, 14362332277634552597, 12612291562289233371, 9068021764334224282, 11003726667849614111, 170500049009536169, 11787850295471586749, 17738376378319933104, 265438126753187088, 16449969716110589415, 4267181961918958684, 8504721844419720345, 3602399335681951800, 16377130351527521329, 137205552767822057, 15076083541717516190, 16933079658536833273, 11539760435976559163, 10349113249022571006, 13506623588121209051, 1767257281718218581, 55497369433803178, 9620183217554454747, 352109299759977748, 13362871402671548794, 3245933715092323519, 7098945802580095824, 4749740144906242542, 16475573756134089178, 17665764356947420150, 2428128185580929142, 10865799872171434959, 14020645350131532589, 10866919792482735515, 1639413999413384841, 2660467607619573650, 7176921049243916372, 44929497464104249, 8302026006819056308, 14088827593384756939, 4541386427308185948, 14992023310005249339, 11521110449882379692, 8618468396936995487, 17255690317020962535, 14459878492479278129, 484161739083752565, 8967126682428339806, 12208164843579773375, 11736932142677088849, 7727530756457513692, 3829808422387045462, 9815185898534079561, 8586014595553015140, 3121180959957037281, 546542310230906996, 12788213799003801890, 6764098612553553982, 16230764669201238834, 18205877184448874064, 17741584570061449195, 13498693246362717293, 12557996638970667763, 16240767280840697248, 12688455377024311919, 11821568382422290340, 13694830011903255027, 15977888673915506876, 12346885892635259078, 7838634663919088845, 13697951298959265290, 16396403340832798324, 5570724586621569543, 348190538972825181, 498434119496336507, 4629603637537989875, 2904956541370261046, 15056806750205280060, 12512751698356956353, 11598492895309981739, 5900963668615601483, 9286588840856606265, 14687331465648814630, 724531149460506959, 17016613597390705501, 17860966464838170961, 8082441243109422217, 4226070025033485357, 11557581090421115709, 1365974406386375567, 11626532849062235723, 3026767794107211866, 18265729906007136324, 9752072017332967624, 8344899021234511823, 17168023990850847933, 2108491903973827339, 16946871590663953204, 15268856540448037497, 6729814538132205074, 10608459573931314294, 5349389425094153624, 9119249437078259281, 3022057742231131843, 699495075963768616, 3938180359891046702, 3132000820601213475, 6453763775620458305, 10361983187468507141, 18091129984666032675, 4573010375750843342, 791243713554231377, 6523321933147523990, 2460943155031244372, 11915079949168514844, 10962272930784254451, 7828398430854164950, 11580373300607261323, 14496114508805667408, 12800088002722989479, 4489382774379581027, 6241885538530491013, 15369736452242646419, 18339907485699833664, 14843607724306799380, 15883998472835946312, 13401911608426527924, 3615974264171478906, 2951259064496198811, 7803436242736563826, 4135188636826481442, 5021264042001895982, 5708915960985917130, 11181910501244483073, 5573954009605843738, 3021445895744683140, 10033196279958934660, 2680855996735532569, 5360189858868901361, 8167521138921792938, 6161893524269697852, 5558764473993615110, 13408224815379298518, 17751136251534065932, 12169040946650623409, 8591752444091873275, 17571132974848304944, 16886102890910720967, 10434431909683674783, 1798513582887417581, 4922950544911394484, 436078592099283889, 10061099463464191790, 2611739359719785328, 12076811020743303539, 2799012545596479383, 12408665237686526887, 2569240801657154200, 189527510828503181, 17204452437985213973, 15873367317020085673, 4668478220806245681, 2950905851413543275, 17244737907264565987, 9947196811151946334, 10861412944742179841, 17691963506930352, 8645426666922253783, 5429177116065336723, 9148166318339274858, 1140817301847500253, 16395024534726001957, 14455719375367518785, 14365592159046307404, 4233672053992875940, 7055944177387857447, 13438827615850026797, 1980459165532258112, 9924227990341676772, 1258768952545009550, 11361136852134788879, 4300533493752614933, 14681866951052377042, 8810851615125798911, 8542930103562314876, 14579475506918455576, 16047523528880779866, 1380610643416544755, 12076763661431463653, 13633351579395427301, 14309637244904670356, 2784919727650036805, 10011701223131936197, 16483582182156980016, 8123259590358566068, 15547670775408355653, 17114873767724596286, 15947690112937005468, 7121267006666076401, 15013329343112101948, 6864703775066800136, 2091646091797307547, 11775971286169844616, 13169145274668540822, 18168794334896751614, 8757043158271235193, 12162217691779194844, 10986813166707328024, 4635742872437686441, 9862874769906586011, 5685640425162748748, 16154828004824450666, 12628559068947614691, 18330543771355967176, 9613516487817756865, 11541501577179857879, 14497414068611647595, 16303734492840330251, 3271500016365005027, 3388428085388242514, 1510190073604428294, 10472797328548283957, 9702728991503878250, 3428420960955188888, 6445224698406122174, 5824974369892172376, 6434707946773025269, 2528556873146891935, 6653952898338236677, 432032921329160914, 11760277815966837524, 9034646482280577053, 2164586012669056137, 2616742534894002775, 942200230707617758, 5327259632525477213, 13158846232145762876, 418213563708326684, 13494580607955344451, 13712793184114793941, 13061962736775979494, 1304785696522982742, 6636575085535497783, 2548707152553606937, 5179609242429207458, 216456340969811386, 8504681751639758545, 18283819579633351371, 8667595238380606433, 15751060841552119650, 10368350373271876373, 2271051687544383713, 9387982608299096176, 5067191246740902300, 2164563749890672481, 1441096478400860673, 1698497919091504741, 7070556267349479512, 12383115351862498978, 4393914787565756921, 4843292715860537520, 1308644180050696570, 14727896807325886230, 5278800618172724513, 12682261375578839563, 2292210517400729441, 4539831393791783686, 11184877751085848181, 10455063755670025488, 4090948952473244180, 16140611536328585842, 4009612709629840807, 11680437954598062018, 7483349842877448300, 15595722655987483, 6218105392300937979, 4230977848731176695, 13608604339767291094, 15450864502883571776, 14522043162137067612, 17407306325856924818, 4319385475362004982, 3602607459242950116, 12919519173298379659, 17034295612889519066, 16366395208098028226, 16902437965740309665, 2976505459482736335, 13462949500218242510, 9986640179928306819, 15767966148754567460, 5987675944577047926, 908917886808113767, 7775521308318543697, 8554839413248075973, 15830102725396509035, 4299599343707193551, 151253289791368809, 2074429061050605186, 7050639080325887498, 7147021929133361313, 17288365729620621043, 13258996835492542256, 9813891614733236908, 18409516239359796503, 6114024626644998222, 5075084268262314250, 9316231926255260786, 5482842808296472097, 9445382679464571342, 341224484511902160, 13784129997188624024, 7368235505308494752, 9538628927204464393, 15343501567237040869, 17821228923098686582, 11856702827887607105, 4609368864524898262, 14712861947435117594, 10899071438470157317, 9590771163252554239, 18239878173866313008, 17348232285102511866, 7979447902828438866, 10189744825270231378, 15897242279714161903, 6814376918912188976, 14160295163213869895, 3756399085747026247, 7851944732036371005, 11096596485883534745, 17528766768147904271, 12327736621720397026, 17199643471105880304, 1457112013787956971, 4273300114441781498, 15938254022202331850, 12502089261484299213, 4148861150304071474, 16774360387122462360, 4693230099623568126, 4923228118836213154, 9672193860921898593, 12031664828792019070, 5538759348099426194, 16607999864018217913, 12801100377914190264, 3714468733303697571, 15066120849955539008, 8667181143710237426, 11054461905529698068, 5000947219599965404, 13679544882732214263, 12329024745774068972, 5097030027906429561, 623294247887615792, 7749632090228054556, 7348314875737386281, 15051320008802373451, 2316565134939415828, 15735407710770638384, 11219541286219768213, 204970242910995613, 2942251758669266767, 2446839436006958427, 5818242570475463614, 13952882162210790154, 1091967561799274001, 815669942787526663, 17619502901620723825, 16225434478481351091, 3458534598924545265, 13105176322289080982, 11660428227784960936, 17456917329772545202, 17370020327039448988, 9872223534315941551, 11134891555868721043, 7366592335535613164, 17901061154562355983, 11133114536770437092, 1216102370074140712, 12369779197340106392, 15587264963667110618, 9839321331851277149, 9504232653874690416, 3277515784377114968, 11059930209112798658, 2233223095276440320, 8766259643725656785, 2981451568249872324, 16923059343824130016, 10424762723653272247, 5892364915443744172, 5076056599547198181, 8353569794147013632, 68280038528939863, 13688795951892474996, 18383293316785491223, 16830221144227410771, 7584798539822253809, 16154968662715915283, 15260829610123279933, 4877893352139268298, 12344113633536211040, 12755524932207520008, 5908761689287331221, 10710685683019125231, 13529779487666749860, 17058207837744409161, 16146404756880670361, 479722120166144953, 18441286007767994888, 291021007503523962, 18404478127831570654, 7161684062922444049, 13215140078849265993, 3557093399709796464, 8888690439305341966, 6505462940112971530, 8788739344222162420, 1559480144085566061, 12347917275519574148, 81829582595789879, 256554008735570761, 13242371414730122957, 11233874231428992467, 13642556384815692603, 15402098527178414517, 11899811780905828512, 17981855746545737550, 4198592355605474429, 5837385946994485658, 8495884884442446152, 14987601548279232776, 8084557976601943459, 1951816494581368991, 9198564418991457621, 7932995247156296394, 1727181807973386737, 6589861619929187838, 8606879269790701257, 4872437793541536276, 15996953415759653811, 9248501959204439487, 4430871643980849717, 14781923535395473967, 15369814218152848270, 8234249513592097579, 17526914633363815278, 12602191579658959446, 14791379194771288560, 5744799145746380430, 16286641132134680583, 14401259673433035989, 8781313506229705992, 15404783223179793847, 1240592003072635453, 6610236446870877009, 13844205871835893697, 5872162931619514680, 7969671272013520825, 2766019064081136959, 12517751573997673572, 9675763639282129596, 6287079859085827340, 13703850028043029227, 2177538632683478842, 6799380297638496469, 18086402650215147822, 6934362201312885542, 18313335318052001373, 11480263463655438919, 9106785110623113711, 7886399579140250642, 3228263571695418855, 16330664963396613091, 17040963948964130546, 10826606124423646728, 2004304733703582220, 6398041571715522263, 493137561871256273, 9640584407491032029, 16021497942534243559, 3278925318796881775, 13963508362353842195, 10912881406340519756, 12333002179163988752, 10955825398678638303, 13098738959421529927, 4516651215445389327, 560548562818360587, 6879446280544278794, 17586026517062529192, 3060809513700298266, 10921253043682209150, 3096750023591656316, 13400270480516947274, 14497399820138619643, 885203573443562232, 14340392236208331243, 2009503763921531273, 5844055580211151684, 11452679420109767541, 9889351505080896698, 12297221479872520074, 145327472993840493, 14415741022760094936, 8161272693495024070, 12628038780375717745, 5651066232426624946, 6800289990668254787, 5629827258100727980, 9532683887081871864, 17078228306713530437, 5752393712365853210, 9906279898480007557, 15575593797821095372, 7944135127159515198, 9274370606751170281, 8181946307601340138, 8855405836683610977, 10604653901416893787, 11825055110857035062, 4735989253296218178, 9585945902650058725, 16832571384429265203, 14392760261562270322, 14439958219835048793, 6845765491294793435, 10537690616100733378, 10290121783493343259, 17074695699105811516, 17508569400297966287, 15411447085789948953, 10245321407074763960, 1474249930147284650, 338858065124110851, 16523709105734298997, 17458843705270839631, 11471295397505031119, 6285176061334214908, 2705374183703063320, 12810847959239174924, 10260721046212143624, 4221085600703449212, 1200019904756589653, 10460179773211533763, 11823018480340155341, 9903187458931297940, 1139978577616698133, 5744593808037898897, 16758300938964610655, 7359351744825865326, 10862900264466009346, 3342859891404368697, 18254401553280819107, 17133307977473573143, 11714571723704738721, 8944205159183890163]
pre = mt19937_64()
pre.from_output(list(map(int, res[:312])))
i = 0
for rand in res[312:]:
a = pre.random()
if int(rand) == a:
i += 1
continue
else:
FLAG = b'DASCTF{' + hashlib.md5(str(a).encode()).hexdigest().encode() + b'}'
print(FLAG)
break
美团 #
easy_RSA #
外面一层是rsa padding attack:
n=0x9371c61a2b760109781f229d43c6f05b58de65aa2a674ff92334cb5219132448d72c1293c145eb6f35e58791669f2d8d3b6ce506f4b3543beb947cf119f463a00bd33a33c4d566c4fd3f4c73c697fa5f3bf65976284b9cc96ec817241385d480003cdda9649fa0995b013e66f583c9a9710f7e18396fbf461cb31720f94a0f79
e=0x3
encrypt_m=0x5f4e03f28702208b215f39f1c8598b77074bfa238dfb9ce424af7cc8a61f7ea48ffbbd5a5e1a10f686c3f240e85d011f6c8b968d1d607b2e1d5a78ad6947b7d3ec8f33ad32489befab601fe745164e4ff4aed7630da89af7f902f6a1bf7266c9c95b29f2c69c33b93a709f282d43b10c61b1a1fe76f5fee970780d7512389fd1
encrypt_m_1=0x5f4e03f28702208b215f39f1c8598b77074bfa238dfb9ce424af7cc8a61f7ea48ffc5c26b0c12bcff9f697f274f59f0e55a147768332fc1f1bac5bbc8f9bb508104f232bdd20091d26adc52e36feda4a156eae7dce4650f83fabc828fdcfb01d25efb98db8b94811ca855a6aa77caff991e7b986db844ff7a140218449aaa7e8
def gcd(a, b):
while b:
a, b = b, a % b
return a.monic()
def franklinreiter(C1, C2, e, N, a, b):
P.<X> = PolynomialRing(Zmod(N))
g1 = (a*X + b)^e - C1
g2 = X^e - C2
print("Result")
result = -gcd(g1, g2).coefficients()[0]
f = open("data.txt", "w")
f.write(str(result))
f.close()
return result
m = franklinreiter(encrypt_m_1, encrypt_m, e, n, 1, 1)
from Crypto.Util.number import *
print(long_to_bytes(m))
# the key is :everything_is_easy_in_this_questionCOPY
得到压缩包密码:everything_is_easy_in_this_question
解开之后是many pad attack,尝试缩小明文和key的table的范围:
from Crypto.Util.number import *
from string import *
print(printable.encode())
TABLE1=ascii_letters+digits+"{}_@#\"| "
TABLE2=b'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ,{} '
data = open("one_time_cipher").read().split(',\n')
data = [long_to_bytes(int(i, 16)) for i in data]
print(data)
key = []
for i in range(26):
tmp_key = b""
for j in TABLE1.encode(): # flag的table
yes = True
for k in range(len(data)):
if len(data[k])<(i+1): break
tmp_m = j^data[k][i]
if long_to_bytes(tmp_m) not in (TABLE2.decode()).encode(): # key的table
yes = False
break
if yes:
tmp_key += long_to_bytes(j)
print(tmp_key)
key.append(tmp_key)
TABLE = b"flag{it_1s_P@dd1n_@nd_p@d}"
for k in range(len(data)):
tmp_key = b""
for i in range(26):
if len(data[k])<(i+1): break
tmp_key += long_to_bytes(TABLE[i]^data[k][i])
print(tmp_key)
# flag{it_1s_P@dd1n_@nd_p@d}COPY
得到flag:flag{it_1sP@dd1n@nd_p@d}
https://github.com/fghcvjk/MT-CTF-2021/tree/master/crypto/easy_RSA
Mar.DASCTF #
threshold #
题目代码如下
#make.sage
import random
flag = bytearray("DASCTF{********************************}".encode())
flag = list(flag)
length = len(flag)
N=53
p=257
q=28019
d=18
f=[1]*19+[-1]*18+[0]*16
random.shuffle(f)
g=[1]*18+[-1]*18+[0]*17
random.shuffle(g)
Q.<x> = Zmod(q)[]
P.<y> = Zmod(p)[]
fx=Q(f)
fy=P(f)
gx=Q(g)
Fqx=fx.inverse_mod(x^N-1)
Fpy=fy.inverse_mod(y^N-1)
hx=(Fqx*gx).mod(x^N-1)
r=[1]*10+[-1]*22+[0]*21
random.shuffle(r)
rx=Q(r)
mx=Q(flag)
ex=(p*rx*hx+mx).mod(x^N-1)
print(ex)
print(hx)
可以发现本题的内容和
2020SCTF-Lattice很像,那么我们可以据此写出exp,不过由于这道题中没有bal_mod,所以也就可以去掉
import random
p = 257
q = 28019
n = 53
Zx.<x> = ZZ[]
e = 7367*x^52 + 24215*x^51 + 5438*x^50 + 7552*x^49 + 22666*x^48 + 21907*x^47 + 10572*x^46 + 19756*x^45 + 4083*x^44 + 22080*x^43 + 1757*x^42 + 5708*x^41 + 22838*x^40 + 4022*x^39 + 9239*x^38 + 1949*x^37 + 27073*x^36 + 8192*x^35 + 955*x^34 + 4373*x^33 + 17877*x^32 + 25592*x^31 + 13535*x^30 + 185*x^29 + 9471*x^28 + 9793*x^27 + 22637*x^26 + 3293*x^25 + 27047*x^24 + 21985*x^23 + 13584*x^22 + 6809*x^21 + 24770*x^20 + 16964*x^19 + 8866*x^18 + 22102*x^17 + 18006*x^16 + 3198*x^15 + 19024*x^14 + 2777*x^13 + 9252*x^12 + 9684*x^11 + 3604*x^10 + 7840*x^9 + 17573*x^8 + 11382*x^7 + 12726*x^6 + 6811*x^5 + 10104*x^4 + 7485*x^3 + 858*x^2 + 15100*x + 15860
h = 14443*x^52 + 10616*x^51 + 11177*x^50 + 24769*x^49 + 23510*x^48 + 23059*x^47 + 21848*x^46 + 24145*x^45 + 12420*x^44 + 1976*x^43 + 16947*x^42 + 7373*x^41 + 16708*x^40 + 18435*x^39 + 18561*x^38 + 21557*x^37 + 16115*x^36 + 7873*x^35 + 20005*x^34 + 11543*x^33 + 9488*x^32 + 2865*x^31 + 11797*x^30 + 2961*x^29 + 14944*x^28 + 22631*x^27 + 24061*x^26 + 9792*x^25 + 6791*x^24 + 10423*x^23 + 3534*x^22 + 26233*x^21 + 14223*x^20 + 15555*x^19 + 3381*x^18 + 23641*x^17 + 2697*x^16 + 11303*x^15 + 6030*x^14 + 7355*x^13 + 20693*x^12 + 1768*x^11 + 10059*x^10 + 27822*x^9 + 8150*x^8 + 5458*x^7 + 21270*x^6 + 22651*x^5 + 8381*x^4 + 2819*x^3 + 3987*x^2 + 8610*x + 6022
def inv_mod_prime(f,p):
T = Zx.change_ring(Integers(p)).quotient(x^n-1)
return Zx(lift(1 / T(f)))
def mul(f,g):
return (f * g) % (x^n-1)
def bal_mod(f,q):
g = list(((f[i] + q//2) % q) - q//2 for i in range(n))
return Zx(g)
def decrypt(e,pri_key):
f,fp = pri_key
a = bal_mod(mul(e,f),q)
d = bal_mod(mul(a,fp),p)
return d
def get_key():
for j in range(2 * n):
try:
f = Zx(list(M[j][:n]))
fp = inv_mod_prime(f,p)
return (f,fp)
except:
pass
return (f,f)
M = matrix(ZZ, 2*n, 2*n)
hh = h.list()
for i in range(n): M[i,i] = 1
for i in range(n,2*n): M[i,i] = q
for i in range(n):
for j in range(n):
M[i,j+n] = hh[(n-i+j) % n]
M = M.LLL()
key = get_key()
l = decrypt(e, key).list()
flag = bytes(l)
print(flag)
son_of_NTRU #
虽然这道题目说的不是NTRU,但是我们还是可以发现题目的代码和NTRU基本类似
#! /bin/bash/env python3
from random import randrange
from Crypto.Util.number import *
from gmpy2 import invert
def gcd(a,b):
while b:
a,b = b,a%b
return a
def generate():
p = getPrime(1024)
while True:
f = randrange(1,(p//2)**(0.5))
g = randrange((p//4)**(0.5),(p//2)**(0.5))
if gcd(f,p)==1 and gcd(f,g)==1:
break
h = (invert(f,p)*g)%p
return h,p,f,g
def encrypt(m,h,p):
assert m<(p//4)**(0.5)
r = randrange(1,(p//2)**(0.5))
c = (r*h+m)%p
return c
h,p,f,g = generate()
from flag import flag
c = encrypt(bytes_to_long(flag),h,p)
print("h = {}".format(h))
print("p = {}".format(p))
print("c = {}".format(c))
那么我们可以直接使用 Soreat_u师傅的脚本进行解密
from Crypto.Util.number import *
def GaussLatticeReduction(v1, v2):
while True:
if v2.norm() < v1.norm():
v1, v2 = v2, v1
m = round( v1*v2 / v1.norm()^2 )
if m == 0:
return (v1, v2)
v2 = v2 - m*v1
h = 70851272226599856513658616506718804769182611213413854493145253337330709939355936692154199813179587933065165812259913249917314725765898812249062834111179900151466610356207921771928832591335738750053453046857602342378475278876652263044722419918958361163645152112020971804267503129035439011008349349624213734004
p = 125796773654949906956757901514929172896506715196511121353157781851652093811702246079116208920427110231653664239838444378725001877052652056537732732266407477191221775698956008368755461680533430353707546171814962217736494341129233572423073286387554056407408816555382448824610216634458550949715062229816683685469
c = 4691517945653877981376957637565364382959972087952249273292897076221178958350355396910942555879426136128610896883898318646711419768716904972164508407035668258209226498292327845169861395205212789741065517685193351416871631112431257858097798333893494180621728198734264288028849543413123321402664789239712408700
# Construct lattice.
v1 = vector(ZZ, [1, h])
v2 = vector(ZZ, [0, p])
m = matrix([v1,v2]);
# Solve SVP.
shortest_vector = m.LLL()[0]
# shortest_vector = GaussLatticeReduction(v1, v2)[0]
f, g = shortest_vector
print(f, g)
f = abs(f)
g = abs(g)
# Decrypt.
a = f*c % p % g
m = a * inverse_mod(f, g) % g
print(long_to_bytes(m))
XCTF华为云专题赛 官方Writeup #
题目源码:https://github.com/huaweictf/xctf_huaweicloud-qualifier-2020
太湖杯 #
Aegis #
整个出题的题目参考了googlectf 2020 Oracle的题目。由于考虑到比赛时长的问题(其实是作者比较菜),基本上是将其中的一个考点拿了出来修改成了当前的题目。针对那个题目比较完整的解法可以参考[这里]( https://github.com/nguyenduyhieukma/CTF-Writeups/blob/master/Google CTF Quals/2020/oracle/oracle-solution.ipynb) 这个地方也有这个算法的比较详细的解释。
算法简介 #
AEGIS 算法是一种AEAD(authenticated encryption with associated data 关联数据的认证加密) 加密。这种算法除了能够提供对指定明文的加密,还能够提供对未加密的关联数据的完整性保证。说通俗一点就是,除了能够对我们发送的需要加密的信息进行加密,同时还提供了对我们明文信息的长度和时间这些未加密的数据进行验证的手法。当我们将密文解开的时候,会包含一个之前提供的明文信息的验证途径,例如能够得到长度的一个验证数据,我们此时就能够用这个数据验证我们之前未加密的长度的完整性。 在题目中,我们能看到两种不同的值:pt和aad
ct, tag = cipher.encrypt(iv, aad, pt)
此处的pt表示的就是我们通常意义下的明文,而这里的aad,实际上就是authenticated associated data,认证关联数据。这个数据会参与到整个加密过程中,用于生成状态。
ct表示的是加密后的密文,tag则是在加密完成后的状态算法中生成的校验标签,可以用来校验aad的值是否发生变化。
关于aad的验证算法可以初步看一下加密过程。
def encrypt(self, iv, ad, msg):
S = self.initialize(iv)
S = self.update_aad(S, ad)
S, ct = self.raw_encrypt(S, msg)
tag = self.finalize(S, len(ad) * 8, len(msg) * 8)
return ct, tag
def decrypt(self, iv, ad, ct, tag):
S = self.initialize(iv)
S = self.update_aad(S, ad)
S, pt = self.raw_decrypt(S, ct)
tag2 = self.finalize(S, len(ad) * 8, len(ct) * 8)
if tag2 != tag:
raise Exception('Invalid tag')
return pt
由于在加密或者解密过程中,aad值参与了最初加密状态的生成,所以aad值在不变的前提下,加解密中状态(State)变化是一致的,最后阶段算出来的 tag2 理论上会和我们传入的tag一致,就是利用这一点来保证aad的完整性。
Aegis128的算法 #
想要明白当前的算法的漏洞,需要先看明白当前加密算法原理。整个加密中会维护一个状态的概念,然后我们需要加密的内容会类似一些向量来影响整个状态,从而对明文完成加密。那么首先,为了更加方便的描述加密过程,我们需要预先定义一些变量:
S[i]: 第i步更新的状态
S[i][j]: 第i步状态中,第j块128bit分组
^: 状态之间异或运算
&: 状态的与运算
const0: 128bit的一个魔数(0x000101020305080d1522375990e97962)
const1: 128bit的一个魔数(0xdb3d18556dc22ff12011314273b528dd)
Aegis有三种不同的加密方式,我们这里使用的是128版本
状态更新 StatusUpdate #
Aegis加密算法中,一个重要的概操作就是状态更新StateUpdate。当这个过程发生的时候,其更新算法如下:
m: 一个128bit的信息
S[i+1] = StatueUpdate(S[i], m)
S[i+1][0] = S[i][0]^AESRound(S[i][4])^m
S[i+1][1] = S[i][1]^AESRound(S[i][0])
S[i+1][2] = S[i][2]^AESRound(S[i][1])
S[i+1][3] = S[i][3]^AESRound(S[i][2])
S[i+1][4] = S[i][4]^AESRound(S[i][3])
这个更新过程的流程大致可以写作如下:
初始化过程 #
整个算法的更新,首先使用密钥K128与初始化向量IV128进行一些运算,最终产生整个算法的初始状态。此时的K128为我们加密算法的密钥,IV128为一个可变的向量。整个生成的过程可以写作:
def initialize(self, iv):
k_iv = _xor(self.key, iv)
S = [k_iv,
self.const_1,
self.const_0,
_xor(self.key, self.const_0),
_xor(self.key, self.const_1)]
for _ in range(5):
S = self.state_update(S, self.key)
S = self.state_update(S, k_iv)
return S
根据代码,我们可以写作:
S[-5][0] = k128^iv128
S[-5][1] = const_1
S[-5][2] = const_0
S[-5][3] = k128^const_0
S[-5][4] = k128^const_1
for i in range(5)
S[-5+i+1] = StatueUpdate(S[-4+i], k128)
S[-5+i+1] = StatueUpdate(S[-4+i+1], k128^iv128)
这里写作-4,主要是为了可以同步,保证我们在起始状态下为S[0]。
Aegis 中的AES #
我们来仔细看一下Aegis中的AES算法。首先来看到官方给出的aes:
def aes_enc(s: block, round_key: block) -> block:
"""Performs the AESENC operation with tables."""
t0 = (te0[s[0]] ^ te1[s[5]] ^ te2[s[10]] ^ te3[s[15]])
t1 = (te0[s[4]] ^ te1[s[9]] ^ te2[s[14]] ^ te3[s[3]])
t2 = (te0[s[8]] ^ te1[s[13]] ^ te2[s[2]] ^ te3[s[7]])
t3 = (te0[s[12]] ^ te1[s[1]] ^ te2[s[6]] ^ te3[s[11]])
s = _block_from_ints([t0, t1, t2, t3])
return _xor(s, round_key)
te0[s[0]],te1[s[1]]这些就相当于是s盒,按照s0,s5,s10,s15这种顺序取值相当于是行位移(shift),取值进行异或就相当于是列混淆(mix_column)。整个过程我们大致写下来就是:
AES(m) = mix_column(shift(Sbox(m)))
实际上就是AES加密算法中,除去密钥交换这一步之后的剩余步骤。并且我们知道,整个Aegis加密中,AES参与的方式为:
if j != 0
S[i+1][j] = AES(S[i][(j+4)%5])
else
S[i+1][j] = AES(S[i][(j+4)%5]) ^ mi
于是我们可以简写成如下的运算:
if j != 0
C = AES(M)
else
C = AES(M)^m
那假设此时,我们的M发生了一些变化,我们这里将变化的差值写作dM,此时有
M1 = M^dM
对M1的加密就可以写成:
if j != 0
C1 = AES(M1) = AES(M^dM)
else
C1 = AES(M1)^m = AES(M^dM)^m
C1、C均为我们可以得到的具体值,如果我们能够通过控制加密的内容,使得dM可控(之后会展示)我们就有机会能够推导出M的值。具体的做法如下:
1. 将C1^C,此时消除了m的影响,存在公式
C1^C = AES(M^dM)^AES(M)
2. AES = mix_column(shift(Sbox(m)))
然而首先我们知道,mix_column本身也是异或运算得到的结果,也就是说满足
mix_column(x)^mix_column(x^dx) = mix_column(dx)
而shift只是位移操作,所以也可满足
shift(x)^shift(x^dx) = shift(dx)
所以实际上可以写作
C1^C = AES(M^dM)^AES(M) = Sbox(M^dM)^Sbox(M)
然而实际上,Sbox运算是可以被爆破的。假设我们能知道dM,那我们只需要爆破16个字节,最终就能推导出M的值
Aegis的加密过程 #
由于Aegis128加密中的最小单位为128bit,也就是16字节,所以加密之前会将当前的明文填充至16的倍数。之后,每16个字节的加密手法如下:
for i in range(0, len16(msg), 16):
Ci = (S2 & S3) ^ S1 ^ S4 ^ mi
Si+1 = StatusUpdate(Si, mi)
注意一个细节,这边为了防止S0的参与导致加密算法被利用,所以在加密过程中故意抛弃了S0。 加密结束之后,更新当前状态块。这里参考一个图可能会更加清晰:
p[i][0]`为我们按照16字节分组的第i组明文输入,`k[0][0]`表示第0组的明文加密得到的密文。这里注意,我们的明文的**第0组实际上参与了第一组密文的生成,并且还影响了第1组的状态**。图上的红框表示的就是,当我们的输入`p[0][0]`发生变化的时候,实际上会影响的状态。从图上可知,当输入`p[0][0]`变化的时候,实际上会影响的是:`s[1][0], s[2][0], s[2][1], k[2][0](这个地方应该写作k[2],可能是图片作者写错了)
参考源码:
def raw_encrypt(S, msg):
ct_blocks = []
for i in range(0, len(msg), 16):
blk = msg[i:i+16]
mask = Aegis128.output_mask(S)
if len(blk) < 16:
mask = mask[:len(blk)]
p = blk + bytes(16 - len(blk))
else:
p = blk
ct_blocks.append(_xor(mask, blk))
S = Aegis128.state_update(S, p)
return S, b''.join(ct_blocks)
def encrypt(self, iv, ad, msg):
S = self.initialize(iv)
S = self.update_aad(S, ad)
S, ct = self.raw_encrypt(S, msg)
tag = self.finalize(S, len(ad) * 8, len(msg) * 8)
return ct, tag
Ageis的漏洞点 #
加密流程中,IV和key都不会更新,并且加密7次。最终目的是让我们求出当使用了空的aad进行了StateUpdate状态后得到的初始状态,也就是状态S[1]。
这一类IV、key不发生变化的题目,其实传达的一个含义就是加密算法本身是不变的,即是说对于加密算法C = F(m),这个F是不变量,而此时的m和C都是已知的,就有机会构造合适的m,从而泄露F中的一些信息
第一步泄露 #
这里重新展示一下之前用来描述加密的那张图,这里我们着重关注的是变化值:
可以看到,当p[0][0]变化的时候,s[1][0], s[2][0], s[2][1], k[2]均会收到影响。这里我们复习一下这几个值的关系:
(1)k[2] = (S[2][2] & S[2][3]) ^ S[2][1] ^ S[2][4] ^ p[2][0]
(2)k[1] = (S[1][2] & S[1][3]) ^ S[1][1] ^ S[1][4] ^ p[1][0]
(3)S[2][0] = AESRound(S[1][4])^S[1][0]^p[1][0]
(4)S[1][0] = AESRound(S[0][4])^S[0][0]^p[0][0]
- 由于(2)我们可以知道,
S[1][0]并不参与到整个加密过程中,所以不会对加密本身有影响,因此k[1]的值不发生变化 - 此时生成的密文
kd[2]虽然发生了变化,但是其变化仅仅是因为S[2][1]发生了变化,因为在StateUpdate中,只有S[2][1]会受到输入的影响,其他的状态并不收到当前的输入状态影响:
这里我们将变化后的p写作dp,并且满足dtp = dp^p,发生了相应变化的变量都加上d的前缀,于是此时有:
kd[2] ^ k[2] = S[2][1] ^ Sd[2][1] = AESRound(S[1][0])^AESRound(Sd[1][0])
此时我们的kd[2] ^ k[2]是已知量。而我们此时知道
(5)AESRound(S[1][0])^AESRound(Sd[1][0]) = Sbox(S[1][0])^Sbox(Sd[1][0])
(6)S[1][0] = AES(S[0][4]) ^ S[0][0] ^ p[0][0]
由于(6)中,S[0][0], S[0][4]在IV和key不变的情况下,即使我们更改p也不会发生变化,所以实际上可以推出
(7)Sd[1][0]^S[1][0] = p[0][0]^dp[0][0] = dtp[0][0]
====> Sd[1][0] = S[1][0] ^ dtp[0][0]
于是我们可以将(5)推到成
(8)Sbox(S[1][0])^Sbox(Sd[1][0]) = Sbox(S[1][0])^Sbox(S[1][0]^dpt[0][0]) = kd[2]^k[2]
在(8)这个算式中,dpt,kd,k三个值我们都知道,于是我们只需要爆破S[1][0]中的16字节即可。
不过经过测试,直接爆破是存在多解的情况,所以我们可以增加一个变化,也就是dpt2,两次的结果综合考虑。经过测试,这种方式能够得到唯一的S[1][0]
def resolve(dk_1, ds_1, dk_2, ds_2):
# here we check the
tmpk = aes.bytes2matrix(dk_1)
aes.inv_mix_columns(tmpk)
aes.inv_shift_rows(tmpk)
d_k1 = aes.matrix2bytes(tmpk)
tmpk = aes.bytes2matrix(dk_2)
aes.inv_mix_columns(tmpk)
aes.inv_shift_rows(tmpk)
d_k2 = aes.matrix2bytes(tmpk)
# result should be unique
res = bytearray(16)
# try to bruce it
for i in range(16):
x1 = set()
for c in range(256):
if aes.s_box[c] ^ aes.s_box[c^ds_1[i]] == d_k1[i] and aes.s_box[c] ^ aes.s_box[c^ds_2[i]] == d_k2[i]:
x1.add(c)
res[i] = x1.pop()
assert(len(res) == 16)
return bytes(res)
进一步泄露 #
由于我们有7次通信机会,目前可以如下安排
- 第一次:我们一口气通信获得
k[0],k[1],k[2],k[3],k[4],此时我们可以将p设置为全0,这样的话能够帮助我们之后更加方便的进行计算 - 第二、三次: 得到
S[1][0] - 第四、五次: 得到
S[2][0] - 第六、七次: 得到
S[3][0]
我们可以如法炮制,通过修改p[1][0],p[2][0],得到S[2][0],S[3][0]。此时我们有公式:
(3)S[2][0] = AESRound(S[1][4])^S[1][0]^p[1][0] ==> 直接逆运算,可得S[1][4]
(9)S[3][0] = AESRound(S[2][4])^S[2][0]^p[2][0] ==> 利用之前的技巧,可得S[2][4]
(10)S[2][4] = AESRound(S[1][3])^S[1][4] ==> 直接逆运算,可得S[1][3]
此时我们就有了S[1][0], S[1][3], S[1][4],并且题目中泄露了S[1][2],所以我们最终利用
(11)C[1] = (S[2][0] & S[3][0]) ^ S[1][0] ^ S[4][0] ^ pt[0]
就能得到最后的S[1][1],此时整个题泄露完成。
import aes
import os
import aegis
from aegis import _xor,_and
from pwn import *
import base64
def R(x):
tmp = aes.bytes2matrix(x)
aes.sub_bytes(tmp)
aes.shift_rows(tmp)
aes.mix_columns(tmp)
return aes.matrix2bytes(tmp)
def invR(x3):
tmp = aes.bytes2matrix(x3)
aes.inv_mix_columns(tmp)
aes.inv_shift_rows(tmp)
aes.inv_sub_bytes(tmp)
return aes.matrix2bytes(tmp)
def resolve(dk_1, ds_1, dk_2, ds_2):
# here we check the
tmpk = aes.bytes2matrix(dk_1)
aes.inv_mix_columns(tmpk)
aes.inv_shift_rows(tmpk)
d_k1 = aes.matrix2bytes(tmpk)
tmpk = aes.bytes2matrix(dk_2)
aes.inv_mix_columns(tmpk)
aes.inv_shift_rows(tmpk)
d_k2 = aes.matrix2bytes(tmpk)
# result should be unique
res = bytearray(16)
# try to bruce it
for i in range(16):
x1 = set()
for c in range(256):
if aes.s_box[c] ^ aes.s_box[c^ds_1[i]] == d_k1[i] and aes.s_box[c] ^ aes.s_box[c^ds_2[i]] == d_k2[i]:
x1.add(c)
res[i] = x1.pop()
assert(len(res) == 16)
return bytes(res)
def encrypt(ph, aad, pt):
ph.sendline(base64.standard_b64encode(pt))
ph.sendline(base64.standard_b64encode(aad))
ct = ph.recvline(keepends=False)
ct = base64.standard_b64decode(ct.decode('utf-8'))
tag = ph.recvline(keepends=False)
tag = base64.standard_b64decode(tag.decode('utf-8'))
return ct, tag
def decrypt(ph, aad, pt, index, ct):
left_index = (index+1)*16
right_index = (index+2)*16
enc, tag = encrypt(ph, aad, pt[2*index-1])
# print("enc[{}:{}]".format(left_index/32,right_index/32))
# print("pt[{}:{}]".format(2*index-1, 2*index))
ct1_2 = enc[left_index:right_index]
# encrypt 3
enc, tag = encrypt(ph, aad, pt[2*index])
# print(pt[2*index])
ct1_3 = enc[left_index:right_index]
# decrypt s10
# print(ct)
# print(ct1_2)
# print(ct)
# print(ct1_2)
dk1 = _xor(ct,ct1_2)
dk2 = _xor(ct,ct1_3)
# split S1/S5
# pt split ,too
s = resolve(dk1, pt[2*index-1][16*(index-1):16*(index)],
dk2, pt[2*index][16*(index-1):16*(index)])
return s
def localTest():
ph = remote("127.0.0.1",'10090')
pt = []
padding = b'\x00'*16
p0 = b'\x00'*16
p1 = b'\x00'*16
p2 = b'\x00'*16
pt.append(p0+p1+p2+padding*2)
# for i in range(1,7):
# pt.append(bytes([i%2+1]*16)+padding)
# for s10
pt.append(bytes([1]*16)+padding+padding)
pt.append(bytes([2]*16)+padding+padding)
# for s20
pt.append(padding+bytes([1]*16)+padding+padding)
pt.append(padding+bytes([2]*16)+padding+padding)
# for s30
pt.append(padding+padding+bytes([1]*16)+padding*2)
pt.append(padding+padding+bytes([2]*16)+padding*2)
iv = ph.recvline(keepends=False)
aad = b''
# encrypt 1
enc, tag = encrypt(ph, aad, pt[0])
print(enc)
ct = []
for i in range(5):
ct.append(enc[i*16:(i+1)*16])
s10 = decrypt(ph, aad, pt, 1, ct[2])
# decrypt 2
s20 = decrypt(ph, aad, pt, 2, ct[3])
# decrypt 3
s30 = decrypt(ph, aad, pt, 3, ct[4])
# s20 = s10 xor R(s14) ==> s14 = invR(s20 xor s10)
s14 = invR(_xor(s20, s10))
# s30 = s20 xor R(s24) ==> s24 = invR(s20 xor s30)
# s24 = s14 xor R(s13) ==> s13 = invR(s14 xor s24)
s24 = invR(_xor(s20, s30))
s13 = invR(_xor(s24, s14))
ph.recvuntil("Oops, something leak:")
s12 = ph.recvline(keepends=False)
print(s12)
s12 = base64.standard_b64decode(s12.decode('utf-8'))
# if pt = 00 then enc1 = (s12&s13) xor s14 xor s11
# -> s11 = enc1 xor s14 xor (s12&s13)
enc1 = enc[16:16*2]
s11 = _xor(s14, _xor(enc1, _and(s12, s13)))
# s15 = _xor(s12, _xor(enc12, _and(s16, s17)))
s1 = s10+s11+s12+s13+s14
ph.sendline(base64.standard_b64encode(s1))
ph.interactive()
if __name__ == "__main__":
localTest()
第五空间2020 有几个脚本可以偷 #
secrets #
从算法中可知满足表达式 $c \equiv a_0 x_1^2 x_2 + a_1 x_0 x_2^2 + a_2 x_1 x_2^2 \mod p$
由同余方程构造一个格子
$$ [1,0,0,0,a0 * k]\ [0,1,0,0,a1 * k]\ [0,0,1,0,a2 * k]\ [0,0,0,1,c * k]\ [0,0,0,0,p * k] $$
为满足LLL算法,k取$2^{32}$,最后即可求出系数secret
p = 11262096115235666933802384984690234504897820609940312496824079226002897675039978540501589954252280529685081417842844576044060586114527797910785935210841729
a0=4466180910473361859350789459675556137864618617420328788169821212611803391878541909630693681804259240992086737964898776136917699083088117808235133334853043
a1=4887981314308588962908319833576800643350454985421459983243096186706959103231201770635994519162313869702469523675537059237606426233167545218659189978781299
a2=6222963447321263242047563972710956077055676498584240298712594187843704642795447140199703936008141098341496844773625746023752040758807620531632616610912213
e=[[0, 2, 1], [1, 0, 2], [0, 1, 2]]
c = 2521258878430983025589687858541798401695147486882642972456698768540389939874205997047593688658001566287798373100962518354180078132561217455997908984321742
k=1<<32
A = Matrix(ZZ,[
[1,0,0,0,a0*k],
[0,1,0,0,a1*k],
[0,0,1,0,a2 *k],
[0,0,0,1,c *k],
[0,0,0,0, p *k]
])
A.LLL()
res =[3463832903,3041163877,2616200387]
c = long_to_bytes(0x0497ca92dff6e21bf2882b100d29660e478a8322d06f2d759c07b7ac865d1090)
key = hashlib.sha256(str(res).encode()).digest()
aes = AES.new(key, AES.MODE_ECB)
print(b'flag{' +aes.decrypt(c) + b'}')
data_protect #
encrypt1 直接分解n
encrypt2 无法完全分解n,但是知道其中一个大素数因子,直接转化为 mod p下的rsa
encrypt3 在Zmod(q) 下求解方程
encrypt4 random的随机数预测,前面encrypt1有192bit,encrypt2有192bit,encrypt3中有612*32bit,刚好满足条件,可以预测出key
encrypt5 继续随机数预测,可以预测出私钥x
import random
from gmpy2 import *
from Crypto.Util.number import *
from Crypto.Cipher import AES
from hashlib import sha256
p=64390888389278700958517837593
n=1428634580885297528425426676577388183501352157100030354079
c=1019989333027273450782579103415892125563412519871045896869
q=n//p
d=invert(65537,(p-1)*(q-1))
print(long_to_bytes(pow(c,d,n)))
c= 51342500906961408103258915228768275415740191204733837976903027942824981857691173079133834015102055031777401227355785897344053403243459544157687793960413113104670769220112095273635970933789525875595068985638845129357985043542698076902996316622632153857669586900278252852715534059153367015654872042990169865039
# n=134949786048887319137407994803780389722367094355650515833817995038306119197600539524985448574053755793699799863164150565217726975197643634831307454431403854861515253009970594684699064052739820092115115614153962139870020206132705821506686959283747802946805730902605814619499301779892151365118901010526138311982
# p = 11616788973244169211540879051135531683500013311175857700532973853592727185033846064980717918194540453710515251945345524986932165003196804187526561468278997
# q=n//p
# # print()
# print(q-p)
# d=invert(65537,(p-1)*(q-1))
# print(long_to_bytes(pow(c,d,n))[:-20])
# a,b=(11616788973244169211540879051135531683500013311175857700532973853592727185033846064980717918194540453710515251945345524986932165003196804187526561468278997,11616788973244169211540879051135531683500013311175857700532973853592727185033846064980717918194540453710515251945345524986932165003196804187526563615762644)
# print((b-a)==2**31-1)
# b'XIAOming'
# b'17810111101'
# b'XIAOming@cmail.com'
c=51342500906961408103258915228768275415740191204733837976903027942824981857691173079133834015102055031777401227355785897344053403243459544157687793960413113104670769220112095273635970933789525875595068985638845129357985043542698076902996316622632153857669586900278252852715534059153367015654872042990169865039
n=134949786048887319137407994803780389722367094355650515833817995038306119197600539524985448574053755793699799863164150565217726975197643634831307454431403854861515253009970594684699064052739820092115115614153962139870020206132705821506686959283747802946805730902605814619499301779892151365118901010526138311982
p = 11616788973244169211540879051135531683500013311175857700532973853592727185033846064980717918194540453710515251945345524986932165003196804187526561468278997
n=p
d=invert(65537,(p-1))
print(long_to_bytes(pow(c,d,n))[:-20])
q=5974434331
key=[[978955513, 2055248981, 3094004449, 411497641, 4183759491, 521276843, 1709604203, 3162773533, 2140722701, 782306144, 421964668, 356205891, 1039083484, 1911377875, 1661230549, 312742665, 3628868938, 2049082743], [3833871085, 2929837680, 2614720930, 4056572317, 3787185237, 93999422, 590001829, 429074138, 3012080235, 2336571108, 831707987, 3902814802, 2084593018, 316245361, 1799842819, 2908004545, 120773816, 2687194173], [3213409254, 3303290739, 742998950, 2956806179, 2834298174, 429260769, 769267967, 1301491642, 2415087532, 1055496090, 690922955, 2984201071, 3517649313, 3675968202, 3389582912, 2632941479, 186911789, 3547287806], [4149643988, 3811477370, 1269911228, 3709435333, 1868378108, 4173520248, 1573661708, 2161236830, 3266570322, 1611227993, 2539778863, 1857682940, 1020154001, 92386553, 3834719618, 3775070036, 3777877862, 2982256702], [4281981169, 2949541448, 4199819805, 3654041457, 3300163657, 1674155910, 1316779635, 66744534, 3804297626, 2709354730, 2460136415, 3983640368, 3801883586, 1068904857, 4178063279, 41067134, 752202632, 3143016757], [3078167402, 2059042200, 252404132, 415008428, 3611056424, 1674088343, 2460161645, 3311986519, 3130694755, 934254488, 898722917, 2865274835, 567507230, 1328871893, 3903457801, 2499893858, 492084315, 183531922], [3529830884, 4039243386, 233553719, 4118146471, 1646804655, 2089146092, 2156344320, 2329927228, 508323741, 1931822010, 579182891, 176447133, 597011120, 3261594914, 2845298788, 3759915972, 3095206232, 3638216860], [3352986415, 4264046847, 3829043620, 2530153481, 3421260080, 1669551722, 4240873925, 2101009682, 3660432232, 4224377588, 929767737, 3729104589, 2835310428, 1727139644, 1279995206, 1355353373, 2144225408, 1359399895], [3105965085, 818804468, 3230054412, 2646235709, 4053839846, 2878092923, 587905848, 1589383219, 2408577579, 880800518, 28758157, 1000513178, 2176168589, 187505579, 89151277, 1238795748, 8168714, 3501032027], [3473729699, 1900372653, 305029321, 2013273628, 1242655400, 4192234107, 2446737641, 1341412052, 304733944, 4174393908, 2563609353, 3623415321, 49954007, 3130983058, 425856087, 2331025419, 34423818, 2042901845], [1397571080, 1615456639, 1840339411, 220496996, 2042007444, 3681679342, 2306603996, 732207066, 663494719, 4092173669, 3034772067, 3807942919, 111475712, 2065672849, 3552535306, 138510326, 3757322399, 2394352747], [371953847, 3369229608, 1669129625, 168320777, 2375427503, 3449778616, 1977984006, 1543379950, 2293317896, 1239812206, 1198364787, 2465753450, 3739161320, 2502603029, 1528706460, 1488040470, 3387786864, 1864873515], [1356892529, 1662755536, 1623461302, 1925037502, 1878096790, 3682248450, 2359635297, 1558718627, 116402105, 3274502275, 2436185635, 771708011, 3484140889, 3264299013, 885210310, 4225779256, 363129056, 2488388413], [2636035482, 4140705532, 3187647213, 4009585502, 351132201, 2592096589, 3785703396, 750115519, 3632692007, 3936675924, 3635400895, 3257019719, 1928767495, 2868979203, 622850989, 3165580000, 4162276629, 4157491019], [1272163411, 1251211247, 357523138, 1233981097, 1855287284, 4079018167, 4028466297, 92214478, 4290550648, 648034817, 1247795256, 3928945157, 1199659871, 397659647, 3360313830, 561558927, 3446409788, 2727008359], [1470343419, 3861411785, 953425729, 65811127, 458070615, 1428470215, 3101427357, 1137845714, 1980562597, 4120983895, 45901583, 2869582150, 427949409, 3025588000, 3231450975, 3313818165, 4015642368, 3197557747], [2452385340, 111636796, 897282198, 4273652805, 1223518692, 3680320805, 2771040109, 3617506402, 3904690320, 77507239, 3010900929, 4099608062, 546322994, 1084929138, 902220733, 4054312795, 1977510945, 735973665], [3729015155, 3027108070, 1442633554, 1949455360, 2864504565, 3673543865, 446663703, 3515816196, 1468441462, 897770414, 2831043012, 707874506, 1098228471, 1225077381, 3622448809, 2409995597, 3847055008, 1887507220], [1839061542, 1963345926, 2600100988, 1703502633, 1824193082, 3595102755, 2558488861, 2440526309, 3909166109, 1611135411, 2809397519, 1019893656, 3281060225, 2387778214, 2460059811, 198824620, 1645102665, 865289621], [224442296, 3009601747, 3066701924, 1774879140, 880620935, 2676353545, 3748945463, 1994930827, 75275710, 3710375437, 4132497729, 3010711783, 3731895534, 2434590580, 3409701141, 2209951200, 995511645, 3571299495], [2337737600, 110982073, 2985129643, 1668549189, 3298468029, 698015588, 2945584297, 1036821195, 4249059927, 3384611421, 3304378629, 1307957989, 602821252, 184198726, 1182960059, 4200496073, 1562699893, 3320841302], [5866561, 2442649482, 479821282, 2687097642, 3347828225, 1876332308, 2704295851, 2952277070, 1803967244, 2837783916, 658984547, 3605604364, 1931924322, 3285319978, 556150900, 3795666798, 261321502, 1040433381], [3855222954, 3565522064, 1841853882, 1066304362, 3552076734, 3075952725, 2193242436, 2052898568, 2341179777, 3089412493, 165812889, 4196290126, 3568567671, 28097161, 2249543862, 1251207418, 522526590, 765541973], [1801734077, 2132230169, 667823776, 3900096345, 3119630138, 3620542178, 2900630754, 30811433, 608818254, 1040662178, 900811411, 3221833258, 43598995, 1818995893, 2718507668, 3445138445, 3217962572, 1437902734], [1812768224, 392114567, 2694519859, 1941199322, 2523549731, 2078453798, 851734499, 2376090593, 2069375610, 4084690114, 246441363, 4154699271, 58451971, 31806021, 4158724930, 2741293247, 3230803936, 2790505999], [3906342775, 2231570871, 1258998901, 1517292578, 162889239, 3130741176, 3925266771, 1780222960, 2378568279, 3873144834, 1597459529, 1581197809, 4101706041, 196019642, 1439141586, 587446072, 2012673288, 1280875335], [4058452685, 653145648, 553051697, 1406542226, 4053722203, 994470045, 2066358582, 3919235908, 2315900402, 3236350874, 172880690, 3104147616, 489606166, 3898059157, 200469827, 665789663, 3116633449, 4137295625], [1460624254, 4286673320, 2664109800, 1995979611, 4091742681, 2639530247, 4240681440, 2169059390, 1149325301, 3139578541, 2320870639, 3148999826, 4095173534, 2742698014, 3623896968, 2444601912, 1958855100, 1743268893], [2187625371, 3533912845, 29086928, 543325588, 4247300963, 1972139209, 272152499, 4276082595, 3680551759, 1835350157, 3921757922, 2716774439, 1070751202, 69990939, 3794506838, 699803423, 3699976889, 40791189], [539106994, 1670272368, 3483599225, 2867955550, 2207694005, 1126950203, 693920921, 2333328675, 539234245, 1961438796, 3126390464, 1118759587, 59715473, 1450076492, 4101732655, 3658733365, 940858890, 1262671744], [3092624332, 2175813516, 3355101899, 3657267135, 770650398, 359506155, 4149470178, 3763654751, 1184381886, 942048015, 523057971, 1098635956, 1732951811, 150067724, 2417766207, 4152571821, 2759971924, 4284842765], [3336022203, 2569311431, 2752777107, 1441977867, 1279003682, 3861567631, 1064716472, 3046493996, 1339401643, 39466446, 1464905290, 420733872, 2057911345, 2418624800, 2193625430, 1558527155, 4224908000, 207684355], [2681129718, 4210889596, 4051161171, 3131196482, 1128312875, 938670840, 2828563599, 3078146488, 1102989364, 3557724304, 156013303, 2371355565, 3608679353, 3513837899, 155622460, 396656112, 2493417457, 876296360], [3135876409, 181875076, 3662181650, 3851859805, 3626146919, 90441351, 1944988720, 585429580, 3158268550, 1399100291, 3688843295, 2851190, 2670576474, 3177735154, 3479499727, 197376977, 1790622954, 2393956089]]
cipher=[595403492, 3329072201, 2030986893, 4171901788, 3978623752, 1983221945, 2446721844, 2357069183, 4157116254, 1084149362, 5164304343, 2285835942, 2562444158, 1580792970, 123176562, 878938066, 1581756453, 5868219323, 2039976783, 734750925, 1594241262, 4167440639, 3051132298, 657904326, 2869165250, 1240654684, 2667941558, 4488763635, 3975062760, 4362407867, 2329286887, 1929259095, 4743673673, 3503908479]
#有限域下求线性方程 key*x=cipher 得到 x=[88,73,65,79,109,105,110,103,64,99,109,97,105,108,46,99,111,109]
x=[88,73,65,79,109,105,110,103,64,99,109,97,105,108,46,99,111,109]
for i in x:
print(chr(i),end='')
print()
from randcrack import RandCrack
rc = RandCrack()
t=[]
for i in key:
for j in i:
t.append(j)
p= 64390888389278700958517837593
p_=64390888389278700958517837503
q= 22186905890293167337018474103
q_=22186905890293167337018474045
pd=bytes_to_long(b'\xf1\x0f\xb5\xb5\xae\xf0\x05\x92BWR\xd0>\x91\x0cv\xbc ]\x81')
d=1644175009
# for qq in range(p_+1,p+1):
# for pp in range(q_+1,q+1):
# rc = RandCrack()
# pp,qq=22186905890293167337018474101 ,64390888389278700958517837515
# rc.submit(pp&0xffffffff)
# rc.submit((pp>>32)&0xffffffff)
# rc.submit((pp>>64)&0xffffffff)
# rc.submit(qq&0xffffffff)
# rc.submit((qq>>32)&0xffffffff)
# rc.submit((qq>>64)&0xffffffff)
# rc.submit(pd&0xffffffff)
# rc.submit((pd>>32)&0xffffffff)
# rc.submit((pd>>64)&0xffffffff)
# rc.submit((pd>>96)&0xffffffff)
# rc.submit((pd>>128)&0xffffffff)
# rc.submit(d)
# for i in range(612):
# rc.submit(t[i])
# r=0
# for i in range(4):
# tt=rc.predict_randrange(0, 4294967295)
# r+=tt<<(32*i)
# key = long_to_bytes(r)
# a = AES.new(key,AES.MODE_ECB)
# cipher = a.decrypt(long_to_bytes(206157860554052840058147052190501816262))
# if(b"." in cipher and b"_" in cipher):
# print(pp,qq,cipher)
rc = RandCrack()
pp,qq=22186905890293167337018474101 ,64390888389278700958517837515
rc.submit(pp&0xffffffff)
rc.submit((pp>>32)&0xffffffff)
rc.submit((pp>>64)&0xffffffff)
rc.submit(qq&0xffffffff)
rc.submit((qq>>32)&0xffffffff)
rc.submit((qq>>64)&0xffffffff)
rc.submit(pd&0xffffffff)
rc.submit((pd>>32)&0xffffffff)
rc.submit((pd>>64)&0xffffffff)
rc.submit((pd>>96)&0xffffffff)
rc.submit((pd>>128)&0xffffffff)
rc.submit(d)
for i in range(612):
rc.submit(t[i])
r=0
for i in range(4):
tt=rc.predict_randrange(0, 4294967295)
r+=tt<<(32*i)
r=0
for i in range(16):
tt=rc.predict_randrange(0, 4294967295)
r+=tt<<(32*i)
r=0
for i in range(16):
tt=rc.predict_randrange(0, 4294967295)
r+=tt<<(32*i)
q,g,h=12978641035734240236103271206089768414668942591886536148174561520305999709207251794343245618040094770557383475160630029074093741713376984903835480969208293, 8720814254745089777252083344348851268520692318828030452122549926748859741402125799736178655620806485161358327515735405190921467358304697344848268434382637 ,12099509832855805422212389412411496487421102553928260849593639134939000597394291986995380611893676422073382092596749292780050077552342507027413423034163272
c1,c2=11037273227249384815270477914945574769214510988660737721762529999297862289189700923584519665480479763578699379894125409227652084419849423696932374103120058, 12087705792059361632307776684083188202195541184973623631541534293387150491895486080323457832843438088187773977539401538646693773152621936983533667985808470
print(long_to_bytes(invert(pow(c1,r,q),q)*c2%q))