[toc]

sm2 #

SM2是 国家密码管理局于2010年12月17日发布的椭圆曲线公钥密码算法。

ecc回顾 #

1. 选取曲线 Ep(a,b)
2. Alice取 基点G和私钥k,计算公钥 pubk.传pubk和G给bob
3. bob计算 C1=M+rK；C2=rG传给alice
4. A接到信息后，计算C1-kC2，结果就是点M

描述一条Fp上的椭圆曲线，常用到六个参量：T=(p,a,b,G,n,h)

p a b用来确定曲线

G为基点，n为点G的阶，h 是椭圆曲线上所有点的个数m与n整除

爱德华曲线简介 #

形如

$x^2+y^2=1-d\cdot x^2 \cdot y^2$

加法 #

p1+p2

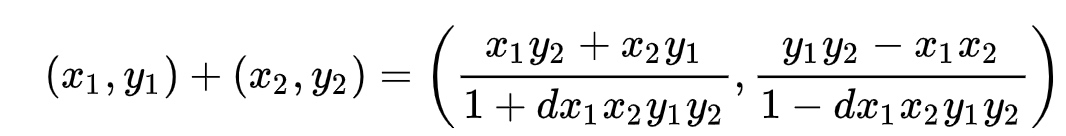
2*p

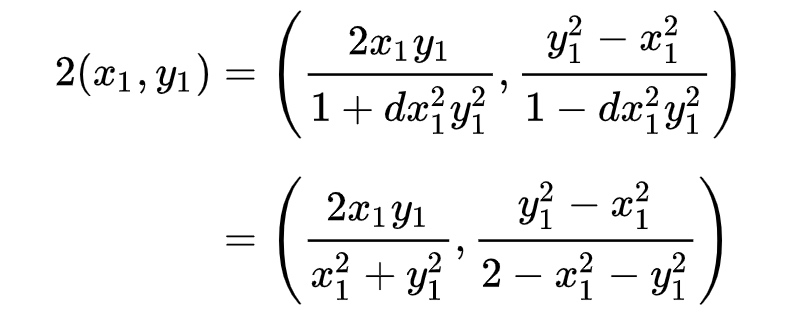
逆元

（x，y）->(-x,y)

零元

（0，1）

爱德华曲线运算的几何意义 #

先考虑常规圆

先建立一个但为远$x^2+y^2=1$

考虑一个爱德华单位曲线

常规爱德华曲线基本性质就这些了

蒙哥马利曲线 Ed25519 签名 #

蒙哥马利曲线（Montgomery curve）是另一种形式的椭圆曲线

常规ecc

$y^2+a_1xy+a_3y=x^3+a_2x^2+a_4x+a_6$

蒙哥马利曲线

$By^2=x^3+Ax^2+x$