↓Skip to main content

基础LFSR 学习

·125 words·1 min
Table of Contents

简单的LFSR模型 #

这是一个 度 m=3 、拥有三个触发器的LFSR

最左边的状态位是在反馈路径中计算得到的

最右边的为输出位

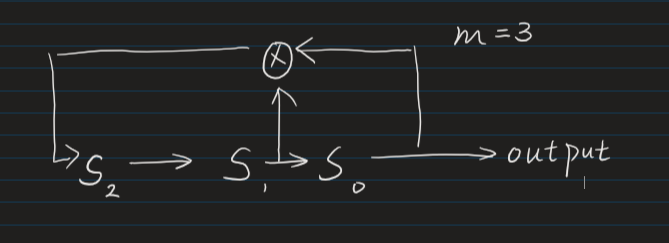
看做下式

def fun(a,b):
    return a^b # （a+b）% 2
while 1:
    output(s0)
    t=feedback(s1,s0)
    s0=s1
    s1=s2
    s2=t

LFSR的通用形式 #

在通用形式中加入了反馈系数 $P$,它决定该反馈器是否会被启用

  • 若 $P$ 为 1 则反馈是活跃的
  • 若 $P$ 为 0 则反馈是关闭的

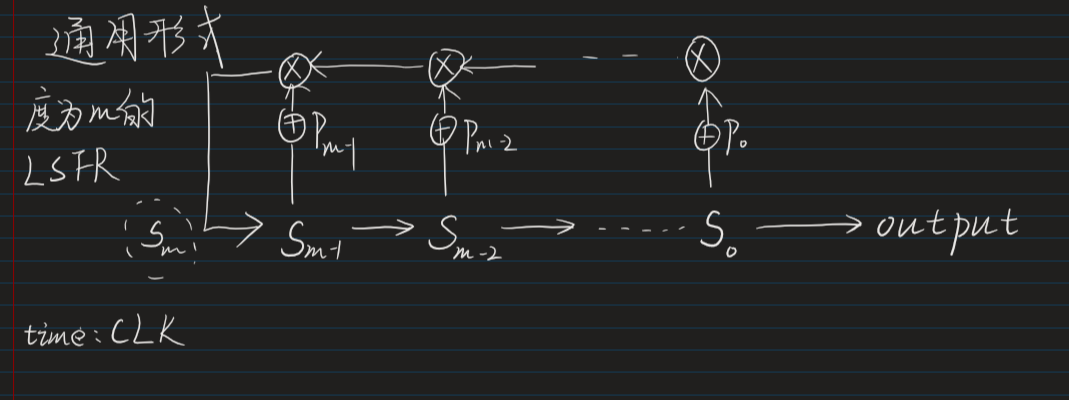
假定LFSR的初始值为 ${S_0},{S_1}…..{S_{m-1}}$

则下一个反馈系数 $S_m$ 就计算式如下

${S_m}={S_{m-1}}\cdot{P_{m-1}}+{S_{m-2}}\cdot{P_{m-2}}……{S_{0}}\cdot{P_{0}};mod;2$

归纳得出整个序列的计算方法为

${S_{i+m}}\equiv\sum_{j=0}^{m-1}P_j\cdot{S_{i+j}};mod;2;;;S_i,P_i\in{0,1};i=1,2….$

序列最大长度为 $2^m-1$

假设已知 m 和部分output 求P #

如果知道 m 的范围可以考虑爆破来做

已知： $$ \begin{cases} {S_m}={S_{m-1}}\cdot{P_{m-1}}+{S_{m-2}}\cdot{P_{m-2}}\cdots{S_{0}}\cdot{P_{0}};mod;2\ {S_{m+1}}={S_{m}}\cdot{P_{m-1}}+{S_{m-1}}\cdot{P_{m-2}}\cdots{S_{1}}\cdot{P_{0}};mod;2\ \vdots\ {S_{2m-1}}={S_{2m-2}}\cdot{P_{2m-3}}+{S_{m-1}}\cdot{P_{m-2}}\cdots{S_{m-1}}\cdot{P_{0}};mod;2\ \end{cases} $$

建立矩阵 #

$$ \begin{pmatrix} S_0 & S_1 & S_2 & \cdots & S_{m-1} & S_{m}\ S_1 & S_2 & S_3 & \cdots &S_{m} & S_{m+1}\ \vdots & \vdots & \ddots & \vdots \
S_{m-1} & S_{m-2} & S_{m-3} & \cdots & S_{2m-2} & S_{2m-1} \end{pmatrix} $$

做法和一般矩阵是一样的，只是把加减法换成异或了

算出来的向量 P

$$ \begin{pmatrix} P_0\ P_1\ \vdots\ P_{m-1}

\end{pmatrix} $$

再用 P 把原模型构造出来

了解整个模型就可以得到整个与加密有关的序列了