养成杯2021

Table of Contents

养成杯2021 #

没有报事后看了一下附件

密码题质量挺水的,只有一个比较有意思的题

RSA? #

这道题拿到就是一个sage文件，给了加密的逻辑

import os

from Crypto.Util.number import *


flag = "GWHT{xxxxxxxxx}"
p = getPrime(256)
q = getPrime(256)
n = p*q
N = (p-1)*(q-1)
e = 65537
Mx = bytes_to_long(os.urandom(30))
My = bytes_to_long(flag)
Z1 = (Mx*My)%n
inv_Z1 = inverse_mod(Z1, n)
inv_2 = inverse_mod(2, n)

X = ((Z1+inv_Z1)*inv_2)%n
Y = My
inv_Y = inverse_mod(Y, n)
a = ((inv_Z1-X)*inv_Y)%n
D = (a*a)%n

xy = lambda (x1,y1),(x2,y2) : ((x1*x2+D*y1*y2)%n, (x1*y2+x2*y1)%n)

def getloop((x,y), e):
        ret = (x, y)
        for i in range(e-1):
               ret = xy(ret, (x,y))
        return ret

print n
print getloop((X, Y), e)
print a

# 13390709926509813526471364597371124446888078365567927211781799241724742352679484983709219580483800891886832613684875066109177882219522305348565532970795023
# (5404548088049249951619519701935576492239293254135836357417714329205323074367876875480850741613547220698045360461761929952847796420174204143917852624050110, 2110372753170830610718226848526649992911771424441223687775304654852191999130502986109306355582366065947895295520226816523397652918227241733632791793362785)
# 1762039418842677123086894939949574689744108610561557889235294034870342076452734215004689409493802437034960516295735815195656138656970901855976802991519141

稍微分析一下有以下式子:

$X=\frac{1+M_x^2M_y^2}{2M_xM_y}$

$Y=M_y$

$a=\frac{1-M_x^2M_y^2}{2M_xM_y^2}$

$D=\frac{(1-M_x^2M_y^2)^2}{4M_x^2M_y^4}$

对getloop稍微分析一下可以发现

n=0时

$X_0=\frac{1+M_x^2M_y^2}{2M_xM_y}$

$Y_0=M_y$

n=1时

$X_1=\frac{1+M_x^4M_y^4}{2M_x^2M_y^2}$

$Y_1=\frac{1+M_x^2M_y^2}{M_x}$

又有

$Y_1a=\frac{1-M_x^4M_y^4}{2M_x^2M_y^2}$

则

$X_1-Y_1a=\frac{2M_x^4M_y^4}{2M_x^2M_y^2}=M_x^2M_y^2$

同理

$X_0-Y_0a=\frac{2M_x^2M_y^2}{2M_xM_y}=M_xM_y$

相当于在

def getloop((x,y), e):
        ret = (x, y)
        for i in range(e-1):
               ret = xy(ret, (x,y))
        return ret

中

每次循环后都会乘上$M_yM_x$

则解一个rsa就完事了

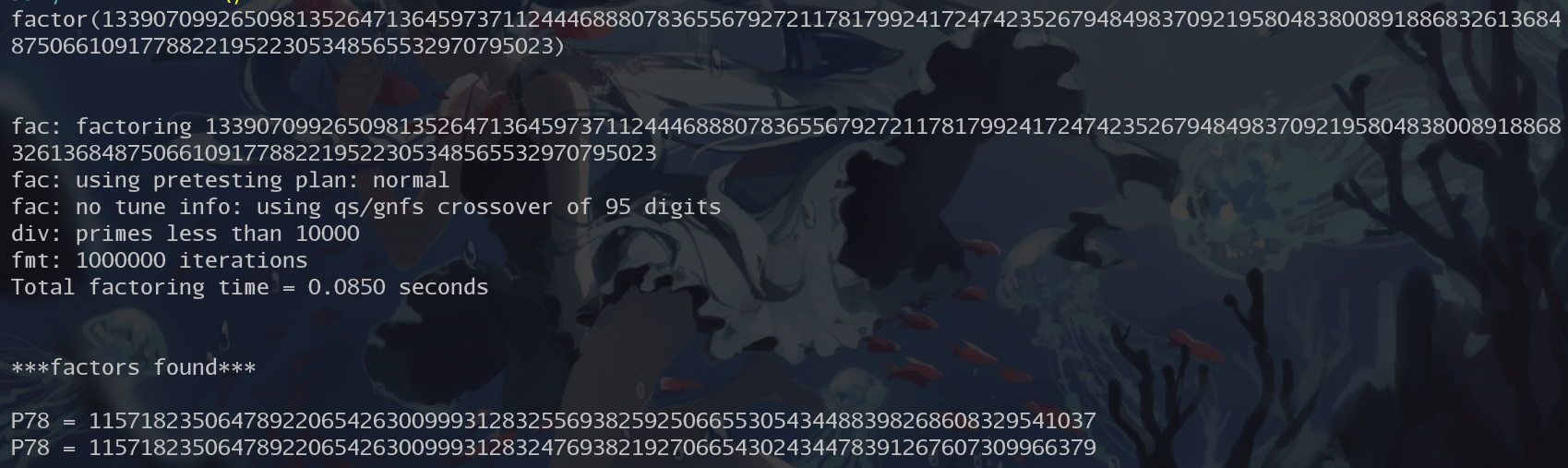
在这个节骨点上👴是万万没想到一个yafu就能把n分解开。。。

solve

import libnum, gmpy2
n = 13390709926509813526471364597371124446888078365567927211781799241724742352679484983709219580483800891886832613684875066109177882219522305348565532970795023
p = 115718235064789220654263009993128325569382592506655305434488398268608329541037
q = n//p
e = 65537
Xn, Yn = 5404548088049249951619519701935576492239293254135836357417714329205323074367876875480850741613547220698045360461761929952847796420174204143917852624050110, 2110372753170830610718226848526649992911771424441223687775304654852191999130502986109306355582366065947895295520226816523397652918227241733632791793362785
a = 1762039418842677123086894939949574689744108610561557889235294034870342076452734215004689409493802437034960516295735815195656138656970901855976802991519141
 
c = (Xn - Yn * a)%n
d = gmpy2.invert(e,(p-1)*(q-1))
xy = pow(c,d,n)
 
flag = ((1-xy*xy)*gmpy2.invert(2,n)*gmpy2.invert(xy,n)*gmpy2.invert(a,n))%n
print(libnum.n2s(flag))

GWHT{pell_equation_is_very_interesting}