L3HCTF2021

Table of Contents

阿巴阿巴，周末白天忙了一整天学校的事，晚上挂机跑了一晚还是没跑出来捏

EzECDSA #

This challenge use SECP256k1 curve to generate the generator ec system

we get 100 sets of signatures and the task.py tells us the low-8bits of K

$S_i = K_i^{-1}(H(m_i)+r_i\cdot dA)\;mod\;n$

leak：$kp = K;mod;256$

and question-44644 on stackexchange says its a problem of Elliptic Curve Digital Signature Algorithm with Partially Known Nonces

In there，known nonce is low-8bits

The idea is to convert the determination of a private key from biased k nonces in several ECDSA signatures into instances of the hidden number problem (HNP), and then solve the HNP as a reduction to the closest vector problem(CVP).

At least ,we kwon we can turn sequence S into a Linear structure

and the answer also tells us,how to turn the equation in a HNP

you can write k as

$k = a + 2^\ell b$

then

$s = (h + rx) \cdot (2^\ell b+a)^{-1}$ $s\cdot (2^\ell b+a) = (h + rx) $ $s\cdot 2^\ell b = h-s\cdot a + rx $ $xr \cdot (2^\ell s)^{-1} = (s\cdot a-h) \cdot (2^\ell s)^{-1} + b$

perfect,without any problem

Define

$t \equiv r\cdot (2^\ell s)^{-1}$ $u \equiv (s\cdot a-h)\cdot (2^\ell s)^{-1}$

and you have

$xt = u + b$

construct sequence

$T=\{t_1,t_2.....t_i\}$ $U=\{u_1,u_2.....u_i\}$

Then,construct a matrix out of basis vectors:

$\begin{pmatrix} q & 0 & 0 & \cdots & 0 & 0 & 0\\ 0 & q & 0 & \cdots & 0 & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & 0 & 0\\ 0 & 0 & 0 & \cdots & q & 0 & 0\\ t_0 & t_1 & t_2 & \cdots & t_n & s_T & 0 \\ u_0 & u_1 & u_2 & \cdots & u_n & 0 & s_U\\ \end{pmatrix}$

which from this article

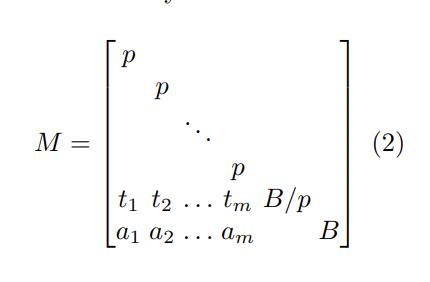
so,we should to find a beautiful B ,Then make

$S_T=B/p$

$S_U=B$

and if you are palying with a good luck

most likely, you’ll see the next-to-last entry of next-to-last row containing a dA or -dA

unfortunately，the lattice in paper seems not very efficient

and @BitLogiK gives a efficient way to make the boundary valid

His way of constructing denotation:

$T_i=2\cdot2^{\ell}\cdot \frac{R_i}{2^{\ell}\cdot S_i} ;mod;n$

$U_i=(2\cdot 2^{\ell}\cdot \frac{KP_i-H_i}{2^{\ell}\cdot S_i} ;mod;n)+n$

$Q’=2\cdot 2^{\ell}\cdot n$

$C_t=1$

$C_u=q$

new lattice looks like this:

$M= \begin{pmatrix} Q' & 0 & 0 & \cdots & 0 & 0 & 0\\ 0 & Q' & 0 & \cdots & 0 & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & 0 & 0\\ 0 & 0 & 0 & \cdots & Q' & 0 & 0\\ T_0 & T_1 & T_2 & \cdots & T_n & C_t & 0 \\ U_0 & U_1 & U_2 & \cdots & U_n & 0 & C_u\\ \end{pmatrix}$

$M {{\;LLL\;or\;BKZ\;}\over \to} B$

then,the privacy will lay in next-to-last col

Obviously,I

def test_result(mat, target_pubkey, curve):
    mod_n = ecdsa_lib.curve_n(curve)
    for row in mat:
        candidate = row[-2] % mod_n
        if candidate > 0:
            cand1 = candidate
            cand2 = mod_n - candidate
            if target_pubkey == ecdsa_lib.privkey_to_pubkey(cand1, curve):
                return cand1
            if target_pubkey == ecdsa_lib.privkey_to_pubkey(cand2, curve):
                return cand2
    return 0

solve #

recv data into a jsonfile and set lattice_attack.py options and get flag by hand

or copy others code to have a happy day 😀

#! python3
import icecream

import string
from icecream import *
from pwnlib.util.iters import mbruteforce
from pwn import *
from hashlib import sha256
from tqdm import tqdm
from rich.progress import track
from rich.traceback import install
install()
# -----------------------------------
table = string.ascii_letters+string.digits
from Crypto.Util.number import *

io = remote('0.0.0.0',23331)
def gopow():
    s=io.recvuntil("XXXX+".encode("utf-8"))
    s=io.recvuntil(")".encode("utf-8"))
    suffix=s[:-1]
    s=io.recvuntil("==".encode("utf-8"))
    s=io.recvuntil("\n".encode("utf-8"))
    cipher=s[1:-1].decode()
    ic(cipher)
    ic(suffix)
    # ic("AAAA".encode() + suffix)
    # ic(sha256("AAAA".encode() + suffix).hexdigest())
    proof = mbruteforce(lambda x: sha256(x.encode() + suffix).hexdigest() == cipher, table, length=4, method='fixed')
    ic(proof)
    io.sendlineafter("Give me XXXX:", proof) 
gopow()



pubkey=eval(io.recvline())
data={}
from tqdm import tqdm
from os import system
data["curve"]="SECP256K1"
data["public_key"]=[pubkey[0],pubkey[1]]
#data["message"]="0".encode("utf-8")
data["known_type"]="LSB"
data["known_bits"]=8
data["signatures"]=[]
for i in tqdm(range(100)):
    io.recvuntil("ge:".encode("utf-8"))
    io.sendline("0".encode("utf-8"))
    io.recvuntil("r =".encode("utf-8"))
    ( ())

    r=int(io.recvline())
    io.recvuntil("s =".encode("utf-8"))
    s=int(io.recvline())
    io.recvuntil("kp =".encode("utf-8"))
    kp=int(io.recvline())
    io.recvuntil("hash =".encode("utf-8"))
    hsh=int(io.recvline())
    (data["signatures"]).append({"r":r,"s":s,"kp":kp,"hash":hsh})
f=open("data.json","w")
import json
f.write(json.dumps(data))
f.close()
system("python3 lattice_attack.py -f data.json")
d=eval(input("plz input the ans\n"))
io.sendline(str(d).encode("utf-8"))
io.interactive()

The curse of ECDSA nonces #

In the question-44644 on stackexchange we know how to solve HNP of bias nonce ecdsa

And Minerva: The curse of ECDSA nonces shows us the attack in detail

Obviously，the primitives is not what we should focus on

remove U to raise speed？

So mul $2^\ell$to T and U to
add a N to U

So，we make make an effort to make the boundary valid? :D