↓Skip to main content

Writeup for crypto in RCTF 2021

·358 words·2 mins Draft
Table of Contents

👴第二次打RCTF，周末又来苟了个水题，👴太极吧菜了，全靠队友带

uncommon1 #

气死了气死了，明明都已经把fastgcd修好了

拿着fastgcd日了半天uncommon2，以为没用，直接扔掉了

淦，根本没考虑过会出现同样的素数，太菜了，明明上课学过的😀😀😀

Fastgcd #

这是个什么玩意呢？

众所周知GCD可以快速的算出两个数最大公约数，但如果有$N$个数我可能要算大概$N^2$次

于是一群数学家想：能不能概一个算法吧它的复杂度降低一点？

大概流程如下

生成树这种概念已经太久远了，👴记不清了

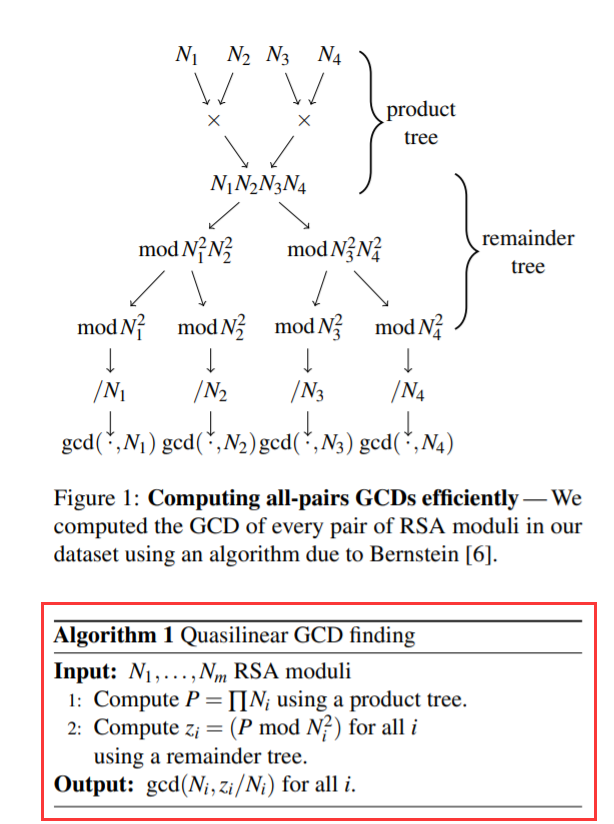
或者长这样：

u神不知在那篇文章找到的实现流程：

文章说复杂度为$O(N(lgN)^2lg(lgN))$

和$N^2$相比就很舒服了

implement #

u神的证明：

完全没想到这一层，上学期还学过，太摆了

fastgcd实现：

你让👴实现这玩意👴肯定是会当场摆烂的，所以👴找到了现成的仓库

https://github.com/sagi/fastgcd

拖下来发现不能立马intsall，于是我们来着手修install

#!/bin/bash

__exists() {
    which $1 1>/dev/null 2>&1
}

get="fetch";
! __exists fetch && get="curl -OL";

if [ ! -d gmp-5.0.5 ];
then

    if [ ! -f gmp-5.0.5.tar.bz2 ];
    then
        $get ftp://ftp.gmplib.org/pub/gmp-5.0.5/gmp-5.0.5.tar.bz2
    fi

    sum=`openssl sha1 gmp-5.0.5.tar.bz2 | awk -F' ' '{print $2}'`

    if [[ $sum != "12a662456033e21aed3e318aef4177f4000afe3b" ]];
    then
        echo ''
        echo '=========================================='
        echo 'ERROR: could not verify gmp-5.0.5.tar.bz2;'
        echo 'Downloaded over untrusted channel (non-https)'
        echo '=========================================='
        exit;
    fi

    tar xf gmp-5.0.5.tar.bz2
fi

cd gmp-5.0.5
patch -p 1 < ../gmp-5.0.5.patch
mkdir ../gmp-patched
./configure --prefix=$PWD/../gmp-patched/
make
make install
cd ..
make

显然是$get ftp://ftp.gmplib.org/pub/gmp-5.0.5/gmp-5.0.5.tar.bz2出了问题（反正我下载不下来）

于是上gmp官网手动下一个

修改install.sh，修改源码报错的预编译代码

fastgcd.c

#define NTHREADS 4 // Get from compile-time argument?

// #ifdef mpz_raw_64 // if patched gmp, use large format int i/o
// #define __mpz_inp_raw mpz_inp_raw_64
// #define __mpz_out_raw mpz_out_raw_64
// #else // otherwise use normal i/o...beware 2^31 byte size limit
#define __mpz_inp_raw mpz_inp_raw
#define __mpz_out_raw mpz_out_raw
// #endif

install.sh

tar xf gmp-5.0.5.tar.bz2
cd gmp-5.0.5
patch -p 1 < ../gmp-5.0.5.patch
mkdir ../gmp-patched
./configure --prefix=$PWD/../gmp-patched/
make
make install
cd ..
make

直接install编译

提取数据为input.modle的格式

from Crypto.Util.number import *
from tqdm import 
size = 2**22
with open("lN.bin","rb") as f:
    data = f.read()

f1 = open("data","w+")
for i in tqdm(range(size)):
    tmp = hex(bytes_to_long(data[i*64:(i+1)*64]))[2:]
    f1.write(tmp+'\n')

开跑~~

结果：

比u神多花了5分钟，还是机子不太行🐨🐨🐨

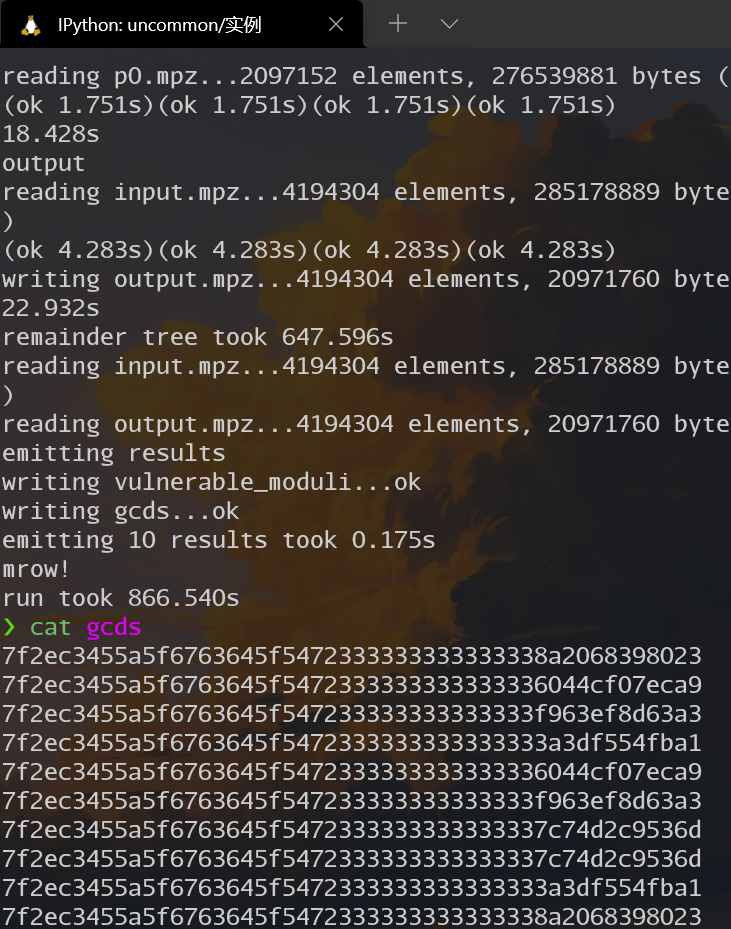
solve # 

In [2]: s=0x7f2ec3455a5f6763645f5472333333333333338a2068398023
   ...:

In [3]: from Crypto.Util.number import *

In [4]: long_to_bytes(s)
Out[4]: b'\x7f.\xc3EZ_gcd_Tr3333333\x8a h9\x80#'

In [5]:

uncommon2 #

A AGCD problem，using lattice reduce is simple to solve it

AGCD #

$n_i=p*q_i+r_i$形式的AGCD问题，利用格规约是可解的

👴看到很多文章都有打法介绍，但是只有这篇介绍了格子的结构（

https://martinralbrecht.wordpress.com/2020/03/21/the-approximate-gcd-problem/

一把梭哈就能解uncommon2

solve # 

#! /usr/bin/sage
from sage.all import *
from sage.groups.generic import bsgs
from Crypto.Util.number import *
from Crypto.Util.number import *
with open("lN.bin","rb") as f:
    data = f.read()

f1 = open("./data","wb")
size = 128
print('size',size)
nn=[]  
for i in range(size):
    nn.append((bytes_to_long(data[i*64:(i+1)*64])))
B = [[0 for i in range(size)] for _ in range(size)]
x0 = nn[0]
B[0][0]=2^305
for i in range(1,size):
    B[0][i]=nn[i]
    # B[0][i]=i
# print(B)
# print(x0)
print('start LLL....')
for i in range(1,size):
    B[i][i]=-x0
B = Matrix(B)
V = B.LLL()
q = abs(V[0][0])

q = q>>305
print(x0-q)
p = x0//q
print(long_to_bytes(p))


# flag{Simpl3_LLL_TrIck}

attachment #

refer #

https://www.usenix.org/system/files/conference/usenixsecurity12/sec12-final228.pdf

https://cr.yp.to/lineartime/multapps-20080503.pdf

https://github.com/sagi/fastgcd