lattice学习
Table of Contents
L3HCTF 2024 #
过年过得好无聊啊
can_you_guess_me_3 #
听说有AGCD,很快啊,我“啪”一下上线了
然后不会
要两次LLL的题
传统无膜AGCD #
先来复习一下不带模的AGCD

直接快进到建造格子
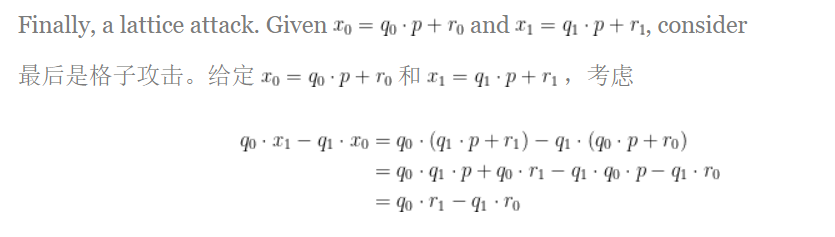
$$ [q_0 \cdot r_1-q_1\cdot r_0 ]=\begin{bmatrix} q_0 & q_1\end{bmatrix}\begin{bmatrix} x_1 \\ -x_0\end{bmatrix} $$
调整一下保证平衡
$$ V=\begin{bmatrix} q_0&q_1\end{bmatrix}\begin{bmatrix} 2^{k+1}&x_1 \\ 0&-x_0\end{bmatrix} $$
再调整一下扩展到n组数据上
那么这个矩阵B就是以前AGCD的解法

求出来的第一行向量就是{v}序列了(不是q序列)
来看一下传统玩法
#! /usr/bin/sage
from sage.all import *
from sage.groups.generic import bsgs
from Crypto.Util.number import *
from multiprocessing import Pool
size = 2^22
flag = open("flag.txt", "rb").read()
assert len(flag) == 22
assert flag[:5] == b"flag{"
assert flag[-1:] == b"}"
seed = flag[5:-1] # 128 bit
seed = (int.from_bytes(seed,'big')<<48) + (randint(0,2^24)<<(128+48)) # 200 bit
ub = seed + 2^48
lb = seed
threads = 64
def f(i):
p = random_prime(ub, lbound=lb, proof=False)
q = random_prime(2**312, proof=False)
N = p*q
return N
def reseed(i):
set_random_seed()
pool = Pool(processes=threads)
pool.map(reseed,range(size))
lN = pool.map(f,range(size))
pool.close()
pool.join()
lN.sort()
with open("lN.bin","wb") as f:
for n in lN:
f.write(int(n).to_bytes(512//8,"big"))
B = Matrix(B)
V = B.LLL()
q = abs(V[0][0])>>(k+1)
带膜AGCD #
from Crypto.Util.number import *
from random import *
from secret import flag
q = getPrime(128)
n = 5
T = 2**48
E = 2**32
t = [randint(1,T) for i in range(n)]
e = [randint(1,E) for i in range(n)]
a = [(t[i] * flag - e[i]) % q for i in range(n)]
print('q =', q)
print('a =', a)
flag = "L3HSEC{" + hex(flag)[2:] + "}"
print('flag =', flag)
# q = 313199526393254794805899275326380083313
# a = [258948702106389340127909287396807150259, 130878573261697415793888397911168583971, 287085364108707601156242002650192970665, 172240654236516299340495055728541554805, 206056586779420225992168537876290239524]
相比之前的情况,加了哥mod q q的大小是512,相对还是比较大的
都是因为加了个膜,不会了涅
用传统思路(上文)构造会卡界
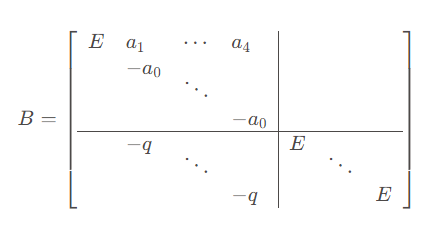
学习 #
通过多多组合算式来获得多个等式
https://tover.xyz/p/2024-L3HCTF-guess/#复盘1
对于常规的AGCD两两组合时,不用处理mod q只需要考虑
$$ \left\{\begin{matrix}a_1=t_1\cdot x-e_1 \\ a_2=t_2 \cdot x-e_2 \end{matrix}\right. $$
$$ \left\{\begin{matrix}a_1\cdot t_2 =t_1 \cdot t_2 \cdot x-e_1 \\a_2 \cdot t_1=t_2 \cdot t_1\cdot x-e_2 \end{matrix}\right. $$
$$ \begin{bmatrix} t_2&t_1\end{bmatrix}\begin{bmatrix} a_1\\-a_2\end{bmatrix}=w $$
加入了q后就要加入一个
$$ a_1\cdot t_2-a_2\cdot t_1=w+k\cdot q \\a_1\cdot t_2-a_2\cdot t_1-k\cdot q=w $$
$$ \begin{bmatrix} t_2&t_1&k\end{bmatrix}\begin{bmatrix} a_1\\-a_2\\-q\end{bmatrix}=w $$
完美
从列来看,组合规律是{a1,a0}、{a2,a0}、{a2,a1}三组
n=3的时候有2+1=3组 N= 3+2+1=6行
n=5的时候有4+3+2+1=10组 N=5+4+3+2+1=15
组合构造,n=3时
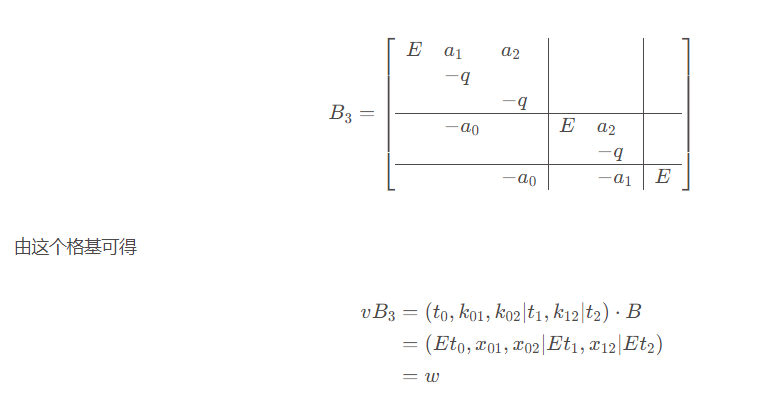
再来分析对角的3个块,都是形如
$$ \begin{bmatrix} E & a_1 & a_2\\ & -q& \\ & &-q\end{bmatrix}\\ \begin{bmatrix} E&a_2 \\ &-q\end{bmatrix} $$
这个式子出来后的结果是 w 序列,乘上B的逆元得到 v={t1,k,k,t2,k,t3}
补习数学 #
计算下界
$$ \sigma(L)= \sqrt{\frac{n}{2\pi e } } \cdot det(L)\approx det(L)=L的体积 $$
用二维举例
$$ L = \begin{bmatrix} 1&2 \\ 2&1\end{bmatrix} $$
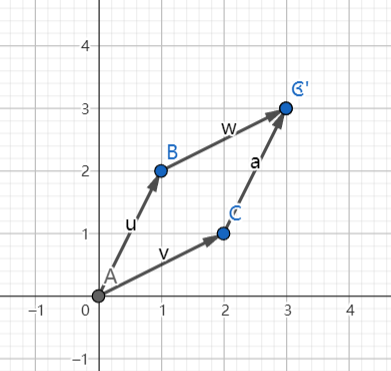
肉眼可见这个向量代表的四边形围城的面积为3
det(L)=3
这个题里面sigma=det(B)^(1/15)=2^1440/15=2^96>2^80=te=2^32*2^48
所以可以吧w回复出来,从而恢复出
$$ T=\{t1,-,-,-,-,t2,-,-,-,t3,-,-,t4,-,t5\} $$
k用-代替
stage2 #
第一步求到了t
下一步求e
$$ a_1\cdot t_0-a_1\cdot t_0-k\cdot q=e_0 \cdot t_1-e_1 \cdot t_0 $$
此时左边全是已知量,这个问题瞬间变得熟悉了起来
$$ \begin{bmatrix} e_0&e_1\end{bmatrix}\begin{bmatrix} t_1\\-t_0\end{bmatrix}=W $$
非常对胃,非常怀念的构造方式
两份思路都是先求t再求e
Coding #
矩阵1:
两两组合很容易得到以下的矩阵
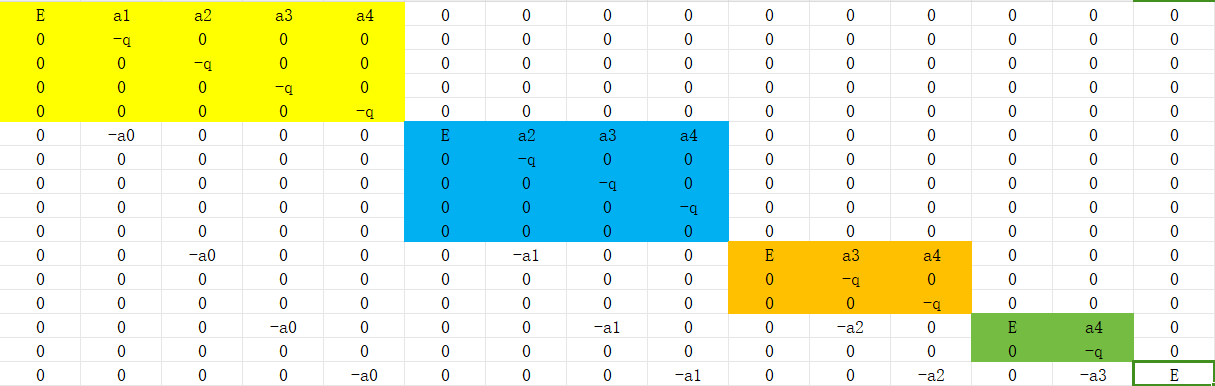
这个前面已经推的差不多了
q = 313199526393254794805899275326380083313
a = [258948702106389340127909287396807150259, 130878573261697415793888397911168583971, 287085364108707601156242002650192970665, 172240654236516299340495055728541554805, 206056586779420225992168537876290239524]
n = 5
T = 2**48
E = 2**32
a0 = a[0]
a1 = a[1]
a2 = a[2]
a3 = a[3]
a4 = a[4]
def matrix_overview(BB):
for ii in range(BB.dimensions()[0]):
a = ('%02d ' % ii)
for jj in range(BB.dimensions()[1]):
if BB[ii, jj] == 0:
a += ' '
else:
a += 'X'
if BB.dimensions()[0] < 60:
a += ' '
print(a)
print()
# stage1
B= [E, a1, a2, a3, a4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, -q, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, -q, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, -q, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, -q, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, -a0, 0, 0, 0, E, a2, a3, a4, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, -q, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, -q, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, -q, 0, 0, 0, 0, 0, 0,
0, 0, -a0, 0, 0, 0, -a1, 0, 0, E, a3, a4, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -q, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -q, 0, 0, 0,
0, 0, 0, -a0, 0, 0, 0, -a1, 0, 0, -a2, 0, E, a4, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -q, 0,
0, 0, 0, 0, -a0, 0, 0, 0, -a1, 0, 0, -a2, 0, -a3, E,]
print(len(B))
BB = Matrix(15,15,B)
matrix_overview(BB)
L = BB.BKZ()
w = L[0]
print("w",w)
v = w * BB^(-1)
print(v)
#
#t0 (-70461467654746,
# -22849328340601, 83526243708890, 107223364615664, 73677848257181,
#t2 -7976473815457,
# 67548140656997, 69391443545774, 55420653404403,
#t3 -179142956465832,
# 63316184541348, 15218068970587,
#t4 -176554799971356,
#t5 -36315145326698,
# -145182873667321)
# t0 X x x x t1 x x x t2 x x t3 x t4
# t应该大于零,对符号取反
t0 =-70461467654746
t1 =-7976473815457
t2 =-179142956465832
t3 =-176554799971356
t4 =-145182873667321
T = [t0,t1,t2,t3,t4]
# a1 a0 a2 a0 a3 a0 a4 a0
K = [-22849328340601, 83526243708890, 107223364615664, 73677848257181,]+[67548140656997, 69391443545774, 55420653404403 ]+[63316184541348, 15218068970587, ]+[-36315145326698, ]
T= [-i for i in T]
K= [-i for i in K]
W = [-i for i in w]
print("T",T)
print("K",K)
v会输出长度为15的短向量,手动处理一下k和t
之前使用的式子是以下式子的左侧,
未知数是ti和k
$$ a_1\cdot t_0-a_0\cdot t_1-k\cdot q=w=e_0 \cdot t_1-e_1 \cdot t_0 $$
由于w已经知道了,未知数变成了e0和e1
把之前分析的步骤再激进一点,右边变成了非常美妙的0
(到这里我感觉其实small root也能做了)
$$ e_0 \cdot t_1-e_1 \cdot t_0-w=0 $$
保险起见左侧矩阵全部设置为正
$$ \begin{bmatrix} e_0&e_1&1\end{bmatrix}\begin{bmatrix} t_1\\-t_0\\-w\end{bmatrix}=0 $$
扩展一下
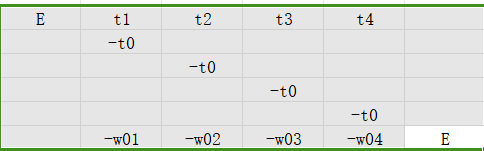
配平:
要让e0E1和-1E在数量级上相近,左上角设置为1右下角设置为e的数量级2**32
w的选取应该是红框位置的列算出的w
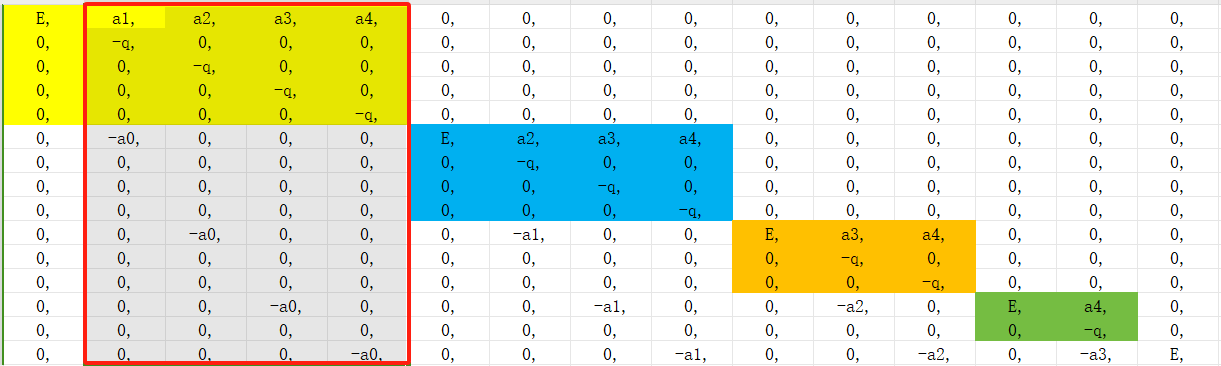
w01 = W[1]
w02 = W[2]
w03 = W[3]
w04 = W[4]
Bs = [1, T[1], T[2], T[3], T[4], 0,
0, -T[0], 0, 0, 0, 0,
0, 0, -T[0], 0, 0, 0,
0, 0, 0, -T[0], 0, 0,
0, 0, 0, 0, -T[0], 0,
0, -w01, -w02, -w03, -w04, -E,
]
B = Matrix(6,6,Bs)
print(B)
L = B.LLL()
w = L[0]
v = w * B^(-1)
assert w[1] == 0
print(v)
# t= [70461467654746, 7976473815457, 179142956465832, 176554799971356, 145182873667321]
# e= [1207385170, 2227664800, 194948058, 2380502097, 893798212]
ok搞到t和e后面后梭哈了
# Ts [70461467654746, 7976473815457, 179142956465832, 176554799971356, 145182873667321]
# es = [1207385170, 2227664800, 194948058, 2380502097, 893798212]
# a = [258948702106389340127909287396807150259, 130878573261697415793888397911168583971, 287085364108707601156242002650192970665, 172240654236516299340495055728541554805, 206056586779420225992168537876290239524]
t0 = 70461467654746
e0 = 1207385170
a0 = 258948702106389340127909287396807150259
x0 = ((a0+e0)*inverse_mod(t0,q))%q
t1 = 7976473815457
e1 = 2227664800
a1 = 130878573261697415793888397911168583971
x1 = ((a1+e1)*inverse_mod(t1,q))%q
print(x1,x0)
flag = x1
flag = "L3HSEC{" + hex(flag)[2:] + "}"
print('flag =', flag)
西湖论剑 2024 #
签个到就溜
MZ #
idapython脚本
base是 v4 = off_1D9000[2 * v5];
off_1D9000数组的偏移,数组是int类型,用dword取,每次4字节
base = 0x001D9078end = 0x01E2CC0ans =[]
for i in range(base,end,4):
tmp = get_wide_dword(i)
ans.append(tmp)
fr = open(r'C:\Users\test_user\Desktop\data\123.txt', 'w')
# 写入数据到文件print(ans,file=fr)
# 关闭文件fr.close()
处理数据,处理off_1D9000的偏移
# 打开文件以写入模式from data import ans
ans2 = []
for i in ans:
if(i>0x01D9078-10):
i-=0x01D9078
ans2.append(i//4)
else:
ans2.append(i)
fr = open(r'C:\Users\test_user\Desktop\data\1234.txt', 'w')
# 写入数据到文件# fr.write(ans)print(ans2,file=fr)
# 关闭文件fr.close()
开始DFS,可能性是可输入的ascii码字符
状态量是flag 、用于sha1验证的v8数组、 数组当前基地址
然后坑爹来了 必须要吐槽一下 哥们用printable作为可能输入跑了一下午
出去买完年货还没跑完,完美错过提交时间
后面看了别人的wp发现有师傅特殊字符只加了_@!~
???
说好的printable呢
看来是我老了
table = digits + ascii_letters + punctuation # 十分钟左右出
table = printable # 跑到天荒地老
from data2 import data2
from string import *
import hashlib
import time
t1 = time.time()
# punctuation = r"""!"#$%&'()*+,-./:;<=>?@[\]^_`{|}~"""
table = "0123456789qwertyuiopasdfghjklzxcvbnmQWERTYUIOPASDFGHJKLZXCVBNM_@!~"
table = "0123456789qwertyuiopasdfghjklzxcvbnmQWERTYUIOPASDFGHJKLZXCVBNM"+"#$%&<=>?@^_~!" # 这两个table都是秒出
cip = "dc0562f86bec0a38508e704aa9faa347101e1fdb"
table = digits + ascii_letters + punctuation #用跟这个久一点
def i2b(m):
if m >= 0:
return m
return 256+m
def dfs(v8,flag,base):
# 是否到底
this_level_possible_chars= []
deep = len(v8)
# print(deep,base)
# print(flag)
if(len(flag)==48):
rinp = []
for i in v8:
rinp.append(i2b(i))
# print(rinp)
tmp = bytes(rinp)
sha = hashlib.sha1(tmp)
hash_str = sha.hexdigest()
# print(hash_str,cip)
if(hash_str == cip):
print(''.join(flag))
t2 = time.time()
print(t2-t1)
return
# printable
# 便利每种路径
for i in table:
v5 = ord(i)
if(base+2 * v5>10000):
break
v4 = data2[base+2 * v5]
# print(v4,v5)
if(v5 - 5 == v4):
v8.append(~(v5 + 1))
flag.append(chr(v5))
next_base = data2[base + 2 * v5+1]
# if(deep<5):
dfs(v8,flag,next_base)
v8.pop()
flag.pop()
this_level_possible_chars.append(chr(v5))
elif(v5 + 5 == v4):
v8.append(~(v5 - 1))
flag.append(chr(v5))
next_base = data2[base + 2 * v5+1]
# if(deep<5):
dfs(v8,flag,next_base)
v8.pop()
flag.pop()
this_level_possible_chars.append(chr(v5))
# print(this_level_possible_chars,deep)
# input()
# "Wrong flag" 无路可走
return
base = 0
v8=[]
flag= []
dfs(v8,flag,base)
t2 = time.time()
print(t2-t1)
(base) PS C:\Users\test_user\Desktop\data> python .\脚本表写.py
Somet1mes_ch0ice_i5_more_import@nt_tHan_effort~!
279.23900842666626