Table of Contents

A study of Cryptanalysis of OCB2 #

Introduction (TL;DR) #

Authenticated encryption (AE) is a term used to describe encryption systems that simultaneously protect confidentiality and authenticity (integrity) of communications; that is, AE provides both message encryption and message authentication of a plaintext block or message .

The offset codebook block cipher mode (OCB)

OCB provide an extremely efficient algorithm, equal to or more efficient than other AE algorithms. OCB is a cipher mode and we can apply ocb to AES/DES/SM4 etc.

The following paragraph briefly introduces OCB1 and OCB2

OCB1 #

Figure 1 shows the overall structure for OCB encryption and authentication.

The message M to be encrypted and authenticated is divided into n-bit blocks, with the exception of the last block, which may be less than n bits. Typically, n = 128.

enc

Input:$(N,M)$

Output:$(C,T)$

The calculation of the Z[i] is somewhat complex and is summarized in the following equations

The operator · refers to multiplication over the finite field $GF(2^{128})$with the irreducible polynomial $m(x) = x^{128} + x^7 + x^2 + 1 $.

The operator ntz(i) denotes the number of trailing (least significant) zeros in i

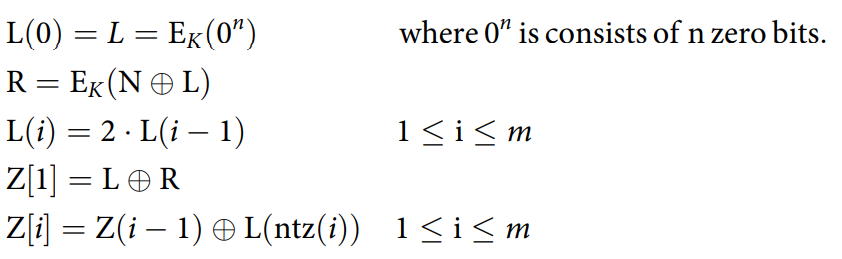
The meanings of other notation are as follows

$checksum = M[1] \oplus M[2] …\oplus Y[m]\oplus C[m]||0*$

$tag = first \; \tau \; bits \; of \; E_K(checksum\oplus Z[m])$

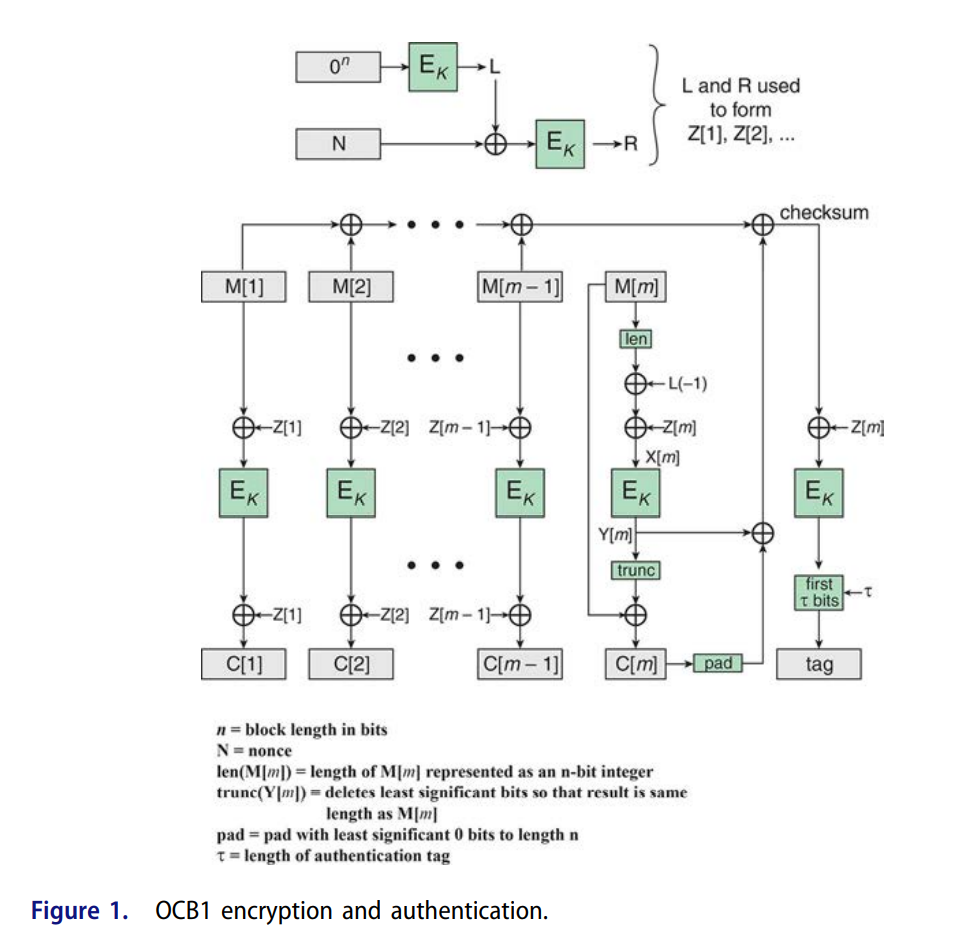
The following figure summarizes the OCB algorithms for encryption and decryption

OCB2 #

We denote with $msb_c(X)$ and $lsb_c(X)$ the first and last c ≤ |X| bits of X respectively.

The mode’s key space K is that of the underlying blockcipher E

the latter is required to have block length n = 128 (in particular, AES is suitable)

the nonce space is $N = {0, 1}^n$

the message space $M$ and the AD space A are the set {0, 1} of strings of arbitrary length

$\sum means \; checksum \; in \; OCB2$

$\epsilon$ means empty

n $len(X)$ denotes an n-bit encoding of |X|,

$D_E(N,A,C,T)$ decrypt the C and use M to recalculate $\sum$

so, T is related with A and M

The main case is the $2^mL$ generation

Basic Attacks (Minimal Forgery Attack) #

We give the minimal example of against OCB2.

The rests are in the attachment

Encrypt $(N, A, M)$ where $N$is any nonce, $A = \epsilon $ is empty, and $M$ is the 2n-bit message

$M = M[1]||M[2]$ where

The encryption oracle returns a pair $(C, T) $consisting of a 2n-bit ciphertext $C = C[1] || C[2]$ and a tag $T$.

constructing parameters are as follows :

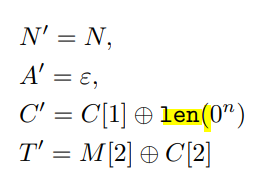
lenth of $C’$ is n,the half of $M$

Decrypt $(N’ , A’ , C’ , T’ ) $

pseudocode:

M[0] (in hex) = 00000000000000000000000000000080
M[1] (in hex) = 0053cc74d9fba8588190c414aff6e6a2

C, T = encrypt(N, M)
C_ = C[0] ^ M[0]
T_ = M[1] ^ C[1]
auth, M_ = decrypt(N, C_, T_)